从零开始学习zk-SNARK(二)-多项式的非交互式零知识证明

even@安比实验室： 上一篇文章中，作者介绍了如何利用多项式的性质来证明某个多项式的知识，相信大家已经对构造证明有了一些基本的认识。目前的证明协议仍然存在一些缺陷，本文将会针对这些薄弱项进行改进，进而最终构造出关于多项式的零知识证明协议。本文重点：KEA，交互式零知识证明，非交互式零知识证明和 Setup。

【本系列文章】

1. 多项式的性质与证明
2. 多项式的非交互式零知识证明
3. 从程序到多项式的构造
4. 多项式的约束
5. Pinocchio 协议

限制多项式

上文说到，多项式的知识其实就是它的系数 c₀ , c ₁ , …, c _i 的知识。协议中我们是通过对秘密值 s 的幂的加密值再进行求幂来对系数进行“赋值”。我们已经限制了 prover 对 s 幂的加密值的选择， 但是这个限制并不是强制的 ，也就是说，prover 可以使用任何可能的方法找到满足下面等式的值 z_p 和 z_h

Z_p =(Z _h ) ^t(s)

再用这两个值来代替 g^p 和 g^h 将它交给 verifier。所以 verifier 需要能够证明 prover 给出的值就是用 s 幂的加密值而不是其它值计算出来的。

我们看一个由一个变量和一个系数组成的一阶多项式的简单例子，对应的 s 的加密值为 E(s) = g^s 。这里我们要做的就是确保 prover 是拿 s 的加密值，即 g^s ，而不是其他值与系数 c 做同态相乘的。所以结果一定是这个形式（c 为任意值）：

(g^s ) ^c

解决这个问题的一种方法就是用另一个“变换”的加密值做同样的操作，充当类似算术中“校验和”（Checksum） 的作用，以此确保结果是原始值的求幂值。

这个是通过 Knowledge-of-Exponent Assumption (简称 KEA) 方法来实现的，在 [Dam91] 中有介绍，更精准一点（注意 a 和 α(alpha)这两个字符的不同）说：

a）Alice 有一个值 a，她想要 Bob 对其进行任意指数的求幂（这里 a 是一个有限域群的生成器），唯一的要求是只能对 a 进行求幂，为了保证这一点，她要：

• 选择一个随机数 α
• 计算 a' = a^α (mod n)
• 提供一个元组 (a, a') 给 Bob, 然后让他对这两个值执行任意的求幂运算，返回结果元组 (b, b')，这里的指数 “α-变换” 依然保持不变，即 b^α = b'(mod n)

b) 因为 Bob 无法从元组 (a, a') 中提取 α 的值，通过暴力破解也难以实现，那就可以推断 Bob 生成有效元组的唯一方法就是执行下面的步骤：

• 选择一个值 c
• 计算 b=(a) ^c (mod n) 和 b' = (a') ^c (mod n)
• 回复 (b,b')

c) 有了回复的元组和 α，Alice 就可以验证等式：

(b)^α = b'

(a^c ) ^α = (a') ^c

a^c·α = (a ^α ) ^c

结论是：

• Bob 在元组的两个值的计算上都用了同一个指数（即 c）
• Bob 只能用 Alice 原本的元组来保持 α 关系
• Bob 知道指数 c，因为构造验证值 (b,b′) 的唯一方式是用同一个指数
• Alice 并不知道 c，这和 Bob 不知道 α 的原因一样
• 虽然 c 是被加密的，但它的可能取值范围并不足够大到保持其零知识的性质，这个问题我们将在后面“零知识”那一节解决。

最后这个协议提供了一个证明给 Alice ，Bob 确实是用他知道的某个值对 a 进行求幂的，而且他也不能做别的任何操作，例如：乘法，加法，因为这样就会破坏 α-变换关系。

在同态加密中，求幂是对被加密值进行乘法运算。我们可以应用这个结构到一个简单的系数多项式 f(x) = c⋅ x的例子中：

• verifier 选择随机数 s, α，然后提供令 x=s 的一阶及其转换的计算值： (g^s , g ^αs )
• prover 代入系数 c 计算： ((g^s ) ^c , (g ^αs ) ^c ) = (g ^cs , g ^αcs )
• verifier 验证： (g^cs ) ^α = g ^αcs

这个结构“限制” prover 只能用 verifier 提供的加密的 s 进行计算，因而 prover 只能将系数 c 赋给 verifier 提供的多项式。现在我们可以扩展这种单项式上的方法到多项式上，因为计算是先将每项的分配分开计算然后再 “同态地” 相加在一起的（这个方法是 Jens Groth 在 [Gro10] 中介绍的）。所以如果给定 prover 一个指数为 s 的幂以及它们的变换的加密值，他就可以计算原始的和变换后的多项式，这里也必须要满足同样的校验。对于阶数为 d 的多项式：

• verifier 提供加密值 $g^{s^0}$ , $g^{s^1}$ ,…, $g^{s^d}$ 和他们的变换 $g^{αs^0}$ , $g^{αs^1}$ ,…, $g^{αs^d}$
• prover:
  • 计算给定的带有 s 的幂的加密多项式 $g^{p(s)} = (g^{s^0})^{c_0} \cdot (g^{s^1})^{c_1}……(g^{s^d})^{c_d} = g^{(c_0s^0+c_1s^1+…+c_ds^d) }$
  • 计算给定的带有 s 的幂的转换的加密“转换”多项式： $g^{αp(s)} = (g^{αs^0})^{c_0} \cdot (g^{αs^1})^{c_1}……(g^{αs^d})^{c_d} = g^(c_0αs^0+c_1αs^1+…+c_dαs^d) = g^α(c_0s^0+c_1s^1+…+c_ds^d)$
  • 将计算结果 $g^p$ , $g^{p'}$ 发给 verfier
• verifier 校验： $(g^p)^α = g^{p'}$

前面的多项式例子 p(x) = x³ - 3x ² +2x 就变成了：

• verifier 提供 $E(s^3)$ , $E(s^2)$ , $E(s)$ 和它们的变换 $E(αs^3)$ , $E(αs^2)$ , $E(αs)$
• prover 计算： $g^p = g^{p(s)} = (g^{s^3})^1 \cdot (g^{s^2})^{(-3)} \cdot (g^s)^2 = g^{s^3} \cdot g^{-3s^2} \cdot g^{2s} = g^{s^3-3s^2+2s}$ $g^{p'} = g^{αp(s)} = (g^{αs^3})^1 \cdot (g^{αs^2})^(-3) \cdot (g^αs)^2 = g^{αs^3} \cdot g^{-3αs^2} \cdot g^{2αs} = g^{α(s^3-3s^2+2s)}$
• verifier 校验： $(g^p)^α = g^{p'}$ $(g^{s^3-3s^2+2s})^α = g^{α(s^3-3s^2+2s)}$ $g^{α(s^3-3s^2+2s)} = g^{α(s^3-3s^2+2s)}$

现在我们就可以确保 prover 是用了 verifier 提供的多项式而不是其它值做计算的了，因为别的方法不能够保持 α-变换。 当然如果 verifier 想要确保在 prover 的多项式中排除了 s 的某些次幂，如 j， 他就不提供对应的密文及其变换：

g^{s ^j} ，g^{αs ^j}

与前面的协议相比，我们现在已经有了一个比较健壮的协议。但是尽管已经做了加密，在零知识 性质上也还依然存在一个很明显的缺陷：即理论上多项式参数 c_ᵢ 是一个很广的取值范围内的值，实际上这个范围可能很有限（比如前面例子中的 6），这就意味着 verifier 可以在有限范围的系数组合中进行暴力破解，最终计算出一个与 prover 的答案相等的结果。比如我们将每个系数的取值范围定为 100，多项式阶数为 2，那么大概会有 100 万种不同的组合，这里可以认为暴力破解只需要少于 100 万次的迭代。更重要的是，即使在只有一个系数，值为 1 的例子中，安全协议也应该能够保证其安全。

even@安比实验室： 有了 KEA，就可以约束 prover 只能通过用 verifier 提供的加密值去构造证明了。严格点讲，这里是用的是 KEA 的扩展版本，叫做 The q-power Knowledge of Exponent Assumption.

零知识证明

因为 verifier 能够从 prover 发送的数据中提取未知多项式 p(x) 的知识 ，那么我们就来看一下这些提供的数据（证明）：

g^p ，g^p' ，g^h

它们参与到了下面的验证：

g^p = (g ^h ) ^t(s) (多项式 p(x) 有根 t(x))

(g^p ) ^α = g ^p' (用了正确形式的多项式)

问题是我们如何选择证明使得这个校验依然有效，同时又保证没有知识能被提取？

前面章节给了我们一个答案：我们可以使用随机值 δ (delta)来“变换”这些值， 如 (g^p ) ^δ 。 现在，为了提取知识，就必须首先要知道一个不可知的值 δ。并且，这种随机化在统计学上与随机值没有什么区别。

为了保持这种关系，我们在 verifier 的检查中验证一下。等式的每一边都有一个 prover 提供的值。所以如果我们用同一个δ 来“变换” 每一个值，那么等式一定保持相等。

具体来讲，就是 prover 选择一个随机值 δ ，并用它对证明中的值进行求幂

$(g^{p(s)})^δ$ , $(g^{h(s)})^δ$ , $(g^{αp(s)})^δ$

然后提供验证内容给 verifier：

$(g^p)^δ = ((g^h)^δ)^{t(s)}$

$((g^p)^δ)^α = (g^{p'})^δ$

再合并一下我们就可以看到校验的等式依然成立：

$g^{δ \cdot p} = g^{δ \cdot t(s)h}$

$g^{δ \cdot αp} = g^{δ \cdot p'}$

注意零知识是如何轻而易举地融入到这个结构中去的，这通常也被称为"无成本的"零知识。

even@安比实验室： 借助这个”无成本的”技巧，就可以轻松实现零知了。但是这里实现零知识的方法和实际中的 Pinocchio 协议，还有 Groth16 方案略有不同。实际方案中是用乘法乘以 $g^{δ\cdot t(s)}$ 。

非交互式

到现在为止，我们已经讲完了一个交互式的零知识方案。但为什么我们还需要有非交互式呢？因为交互式证明只对原始的 verifier 有效，其他任何人（其他的 verifier）都不能够信任这个证明，因为：

• verifier 可以和 prover 串通，告诉他密码参数 s, α，有了这些参数 prover 就可以伪造证明，就像前面 remark 3.1 提到的那样。
• verifier 也可以使用同样的方法自己伪造证明。
• verifier 必须保存 α and t(s) 直到所有相关证明被验证完毕，这就带来了一个可能造成秘密参数泄漏的额外攻击面。

因而 prover 就需要分别和每个 verifier 做交互来证明一个陈述（就是例子中指的多项式的知识）。

尽管交互式证明也有它的用处，例如一个 prover 只想让一个特定的 verifier （称为目标 verifier，更多的信息参见 [JSI96] ）确信，就不能再重复利用同一个证明去向别人证明这个声明了，但是当一个 prover 想让众多的参与者同时或者永久地确信的话，这种方法就很低效了。 prover 需要保持一直在线并且对每一个 verifier 执行相同的计算。

因而，我们就需要一个可以被重复使用，公开，可信，又不会被滥用的秘密参数。

我们先来思考一下如何在构造出秘密值 (t(s),α) 构造之后保证它的安全性。我们可以对其进行加密，方式与 verifier 在发送加密值给 prover 之前对 s 的幂使用的加密方式一致。但是 remark 3.2 中提到，我们使用的同态加密并不支持两个秘密值相乘，这一点对 t(s) 和 h 的加密值相乘以及 p 和 α 的加密值相乘的验证都很重要。这个问题适合用 Pairing 配对操作来解决。

even@安比实验室：这里非交互的证明协议将对参数加密，但引入了两个问题：

1）同态加密无法对两个加密值做乘法，那如何验证加密后的参数呢？

2）加密值一旦泄露，协议的信任关系将无法保证，如何确保参数的安全性？

加密值的相乘

配对操作（双线性映射）是一个数学结构，表示为函数 e(g,g)，它给定一个数据集中的两个加密的输入（即 g^a , g ^b ），可以将他们确定性地映射到另一组不同的输出数据集上的它们的乘积，即 e(g^a , g ^b ) = e(g, g) ^ab ：

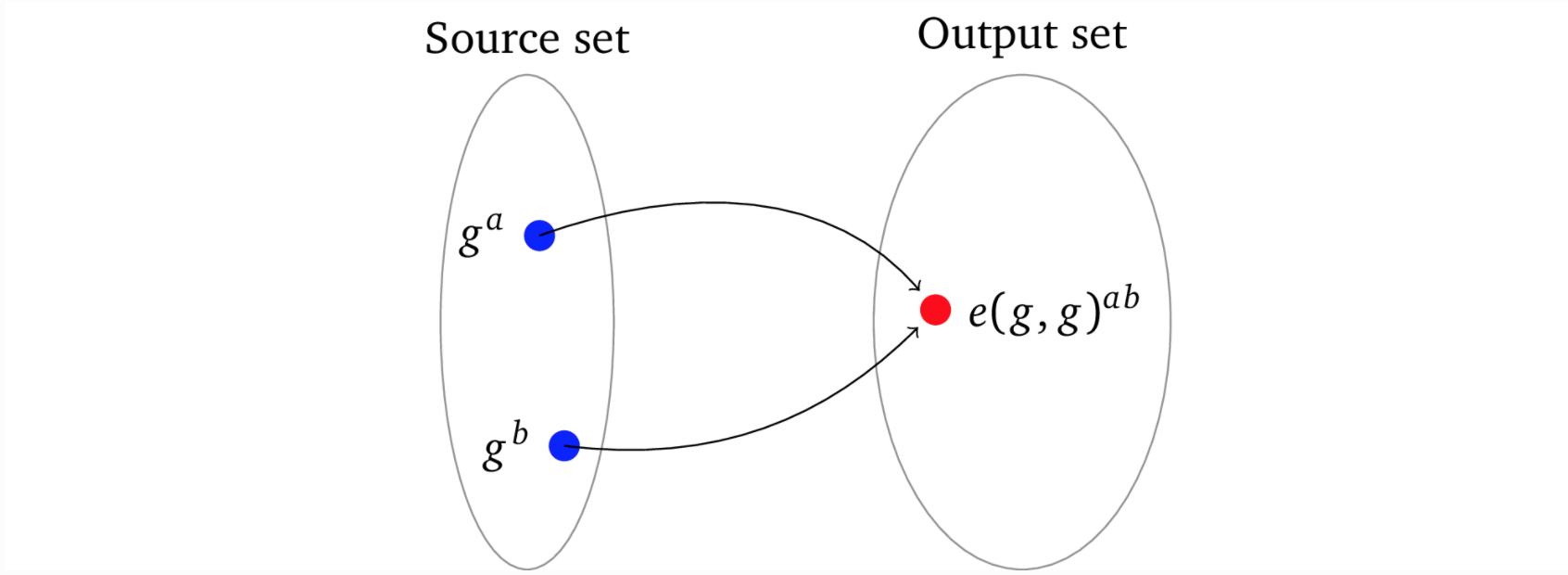
因为源数据集和输出数据集（通常被称为一个 group）是不同的，所以一个配对的结果不能用做其他配对计算的输入。我们可以将输出集（也称为“目标集”）视为“不同的宇宙”。因而我们不能用另一个加密值乘以结果，而且配对这个名称本身也表明了，我们一次只能将两个加密值相乘。

even@安比实验室： 换句话说，配对只支持 x y 这种两个值的乘法，但不支持三个或以上的值相乘，比如不支持 x y * z。

在某种意义上，这个类似于一个哈希函数，他将所有可能的输入值映射到可能的输出值的集合中的一个元素上，通常情况下这个过程是不可逆的。

注意：乍一眼看过去，这个限制可能会阻碍相关功能的实现，但在 zk-SNARK 中这反而是保证安全模式的最重要性质，参见remark 3.3。

配对函数 e(g,g) 可以初步（严格来说是不对的）地类比成“交换”每一个输出的基数和指数的操作，使得基数 g 在交换过程中被修改成了指数的方式，即 g^a → a ^g 。"被转换"的两个输入一起被修改了，这样原始值 a 和 b 就在同一个指数下相乘了，即：

$e(g^a,g^b) =a^g \cdot b^g =(ab)^g$

因而因为基数在“转换”中被修改了，所以在另一个配对中不能再使用这个结果 (ab)^g （即：e((ab)ᵍ, gᵈ)）构造出想要的加密乘积 abd 了。配对的核心性质可以表示成下面的等式：

$e(g^a,g^b) =r(g^b,g^a)=e(g^{ab},g^1)=e(g^1,g^{ab}) =e(g^1,g^a)^b =e(g^1,g^1)^{ab}$

严格来讲一个配对的结果是在目标集的一个不同生成元 g 下对原始值乘积的加密，即 e(g^a , g ^b ) = g ^ab 。因而它具备同态加密的性质，也就是说我们可以把乘法配对的加密乘积放到一起：

$e(g^a,g^b) \cdot e(g^c, g^d) = g^{ab} \cdot g^{cd} =g^{ab+cd} =r(g,g)^{ab+cd}$

注意：配对操作是通过改变椭圆曲线来实现这些性质的，现在我们用的符号 g ⁿ 就代表曲线上一个由生成元自相加了 n 次的点，而不是我们前面用到的乘法群生成元。

[DBS04] 这个综述提供了学习配对的出发点。

可信任参与方的 Setup

有了配对，我们现在就准备去设置安全公开且可复用的参数了。假定一下我们让一个诚实的参与方来生成秘密值 s 和 α。只有 α 和所有必要的 s 的幂及其对应的 α-变换被加密了，那么原始数据就必须要被删除（ i 为 0，1,…,d ）：

$g^α，g^{s^i}，g^{αs^i}$

g^α ，g^{s ⁱ} ，g^{αs ⁱ}

这些参数通常被称为 common reference string 或者 CRS。CRS 生成后，任何的 prover 和任何的 verifier 都可以使用它来构造非交互式的零知识证明协议。CRS 的优化版本将包含目标多项式的加密值 g^t(s) ，尽管这个值并不重要。

把 CRS 分成两组（ i 为 0，1,…,d ）：

• proving key（也被称为 evaluation key）： $(g^{s^i},g^{αs^i})$
• verification key： $(g^{t(s)},g^α)$

只要能够乘以加密值，verifier 就可以在协议的最后一步验证多项式了：

• 有了 verification key，verifier 就可以处理从 prover 那里得到的加密多项式的值 $g^p$ ， $g^h$ ， $g^{p'}$ ：
  • 在加密空间中校验 p = t·h： $e(g^p,g^1) = e(g^t,g^h)$
  • 校验多项式的限制： $e(g^p,g^α) = e(g^{p'},g)$

信任任意一个参与者

尽管受信任设置很有效率，但众多 CRS 用户也必须要相信生成者确实删除了 α 和 s ，这一点没有办法证明（proof of ignorance 是一个正在积极研究的领域 [DK18]），所以这种方法依然是无效的。因而很有必要去最小化或者消除这种信任。否则一个不诚实的参与方就可以构造假证明而不被发现。

一种解决办法就是由多个参与方使用前面小节中介绍的数学工具来生成一个组合式 CRS，这样这些参与方就都不知道「秘密」了。下面是一个实现方案，我们假设有三个参与者 Alice，Bob 和 Carol ，对应为 A，B 和 C，其中 i 为 1, 2, …, d：

• Alice 选择随机数 $s_A$ 和 $α_A$ ，然后公开她的 CRS： $(g^{s^i_A}，g^{α_A}，g^{α_As^i_A})$
• Bob 选择他的随机数 $s_B$ 和 $α_B$ ，然后通过同态乘法结合 Alice 的 CRS： $((g^{s_A^i})^{sB^i},(g^{α{A}})^{α_B},(g^{α_As_A^i})^{α_Bs_B^i}) = (g^{(s_As_B)^i},g^{α_Aα_B},g^{α_Aα_B(s_AsB)^i})$ 然后公开两方 Alice-Bob 的 CRS 结果： $(g^{s^i{AB}},g^{α{AB}},g^{α{AB}s^i_{AB}})$
• Carol 用她的随机数 $s_C$ 和 $αC$ 做同样的事： $((g^{s^i{AB}})^{s^iC},(g^{α{AB}})^{αC},(g^{α{AB}s^i_{AB}})^{α_Cs^i_C}) = (g^{(s_As_Bs_C)^i},g^{α_Aα_Bα_C},g^{α_Aα_Bα_C(s_As_BsC)^i})$ 然后公开 Alice-Bob-Carol 的 CRS: $(g^{s^i{ABC}},g^{α{ABC}},g^{α{ABC}s^i_{ABC}})$

这个协议最后我们就获得了一个混合的 s ⁱ 和 α：

$s^i=s^i_As^i_Bs^i_C, α=α_Aα_Bα_C$

除非他们串谋，否则参与者们互相之间并不知道其他人的秘密参数。实际上，一个参与者必须要和其它所有的参与者串谋才能得到 s 和 α，这样在所有的参与者中只要有一个是诚实的，就没有办法伪造证明。

注意：这个过程可以被尽可能多的参与者重复完成

有一个问题是如何验证参与者在生成 CRS 时用的随机数值是一致的，因为攻击者可以生成多个不同的随机数 s₁, s₂, … 和 α₁, α₂, …，然后代入这些不同的随机数去执行 s 的不同次幂计算（或提供随机数作为一个 CRS 的扩充），从而使 CRS 无效或者不可用。

庆幸的是，因为我们可以使用配对来乘以加密值，所以我们就可以从第一个参数开始逐一执行一致性校验，并且确保了每个参数都源于前一个。

• 我们用 s 的 1 次幂作为标准来校验每一个其它次幂的值与之是否保持一致 $e(g^{s^i},g) = e(g^{s^1},g^{s^{i-1}})|_{i\in{2,……,d}}$ 例如：
  • 2 次幂： $e(g^{s^2},g) = e(g^{s^1},g^{s^1}) => e(g,g)^{s^2} = e(g,g)^{s^{1+1}}$
  • 3 次幂： $e(g^{s^3},g) = e(g^{s^1},g^{s^2}) => e(g,g)^{s^3} = e(g,g)^{s^{1+2}}$ ，等
• 我们现在再验证一下前面步骤中 α-变换后的值是否正确： $e(g^{s^i},g^α) = e(g^{αs^i},g)|_{i\in[d]}$ 例如：
  • 3 次幂： $e(g^{s^3},g^α) = e(g^{αs^3,g}) => e(g,g)^{s^3 \cdot α} = e(g,g)^{αs^3}$ ，等。

这里 $i \in {2,……,d}$ 是“i 值分别为 2，3，…，d” 的缩写， [d] 是 1, 2, …, d 这个范围的缩写形式，在后面的章节这种表示方式更为常见。

当我们在验证每一个参与者秘密参数的一致性时，要注意参与者生成 CRS 的过程并没有强制后一个参与者（就是我们例子中的 Bob 和 Carol）都要使用前面已经公开的 CRS。因而如果一个攻击者是链上的最后一个参与者，他可以像链上的第一个参与者一样忽略前面的 CRS 随便构造一个有效的 CRS，这样他就变成了唯一一个知道秘密 s 和 α 的人。

为了解决这个问题，我们可以额外再要求除了第一个以外的每一个参与者去加密然后公开他的参数。例如，Bob 同样公开了：

$(g^{s^i_B},g^{α_B},g^{α_Bs^iB})|{i\in[d]}$

这就可以去验证 Bob 的 CRS 是乘以了 Alice 的参数后正常获得的，这里 i 为 1, 2,…, d。

• $e(g^{s^i_{AB}},g) = e(g^{s^i_A},g^{s^i_B})$
• $e(g^{α_{AB}},g) = e(g^{α_A},g^{a_B})$
• $e(g^{α{AB}s^i{AB}},g) = e(g^{α_As^i_A},g^{α_Bs^i_B})$

同样的，Carol 也必须证明她的 CRS 是乘以了 Alice-Bob 的 CRS 后正常获得的。

这是一个健壮的 CRS 设置模式，它并不完全依赖于单个参与者。事实上，即使其它所有的参与者都串谋了，只要有一个参与者是诚实的，他能够删除并且永远不共享它的秘密参数，这个 CRS 就是有效的。所以在设置 CRS （有时候被称为仪式 [Wil16]的时候有越多不相关的参与者参与，伪造证明的可能性就越低。当有相互竞争的参与方参与的时候，就几乎不可能伪造证明了。这种模式能够包容其他一些怀疑这种 setup 可识别性的不受信方因为校验步骤确保了他们不会破坏（这里也包括很弱的 α 和 s 的使用）最终的 CRS。

even@安比实验室： 现在有一些 zkSNARK 方案支持可升级的 CRS，任何怀疑 CRS 的参与方都可以对 CRS 进行更新。此外还有一些 zkSNARK 方案支持 Universal CRS，用不着对每一个电路进行受信任设置，而是只需要全局完成一次即可。除此之外，大量无需 Trusted Setup 的方案正在被充分研究。

多项式的 SNARK

我们现在准备来合并这个逐步演化出来的 zk-SNARKOP 协议。为简洁起见，我们将使用大括号来表示由旁边的下标填充的一组元素，例如：

${s^i}_{i\in[d]}$

表示一组数 s ¹ ，s ² ， …， s^d 。我们已经明确目标多项式 t(x) 和 prover 的多项式阶数 d：

• Setup
  • 挑选随机值 s，α
  • 计算加密值 $g^α$ 和 ${g^{s^i}}{i\in[d]}$ ， ${g^{αs^i}}{i\in{0,…,d}}$
  • 生成 proving key： $({g^{s^i}}{i\in[d]},{g^{αs^i}}{i\in{0,…,d}})$
  • 生成 verification key: $(g^α，g^{t(s)})$
• Proving
  • 分配系数 ${ci}{i\in{0,…,d}}$ (即知识)得 $p(x) = c_dx^d +…+ c_1x^1 + c_0x^0$
  • 求多项式 $h(x) = p(x)/t(x)$
  • 代入 ${g^{s^i}}_{i\in[d]}$ 计算多项式 $g^{p(s)}$ 和 $g^{h(s)}$ 的值
  • 代入 ${g^{αs^i}}_{i\in[d]}$ 计算变换多项式 $g^{αp(s)}$ 的值
  • 选择随机数 δ
  • 构造随机化的证明 $π = (g^{δp(s)},g^{δh(s)},g^{δαp(s)})$
• verification
  • 映射证明 π 为 $(g^p,g^h,g^{p'})$
  • 验证多项式约束： $e(g^{p'},g) = e(g^p,g^α)$
  • 验证多项式系数： $e(g^p,g) = e(g^{t(s)},g^h)$

Remark 3.3 如果 pairing 的结果有可能在其它类似的乘法协议中被复用，那么这里就完全没有安全性可言了，因为这样的话 prover 就可以构造

$g^{p'} = e(g^p,g^α)$

这样也可以通过"多项式约束"的检查：

$e(e(g^p,g^α)，g) = e(g^p,g^α)$

结论

我们用 zk-SNARK 协议来解决多项式问题的知识，不过这是一个有局限的例子。因为大家可以说 prover 只要用另外一个有界的多项式去乘以 t(x) 就可以很容易得构造出一个能够通过测试的多项式 p(x) ，并且这种结构也是有效的。

verifier 知道 prover 有一个有效的多项式，但是并不知道是哪一个。我们可以利用多项式的其他性质添加额外的证明，如:被多个多项式整除，是某个多项式的平方。虽然可能会有一个服务能够接受，存储和奖励所有经过证明的多项式，或者有一个需求，加密计算某种形式的未知多项式。然而若有通用方案就可以支撑无数的应用。

even@安比实验室：总结一下这篇文章中一步一步解决了下面的几个问题：

保证 prover 的证明是按照规则正确构造的 ——> KEA

保证知识的零知性 ——> “无成本的”δ 变换

可复用证明 ——> 非交互式

非交互中如何设置安全公开且可复用的参数 ——> 参数加密，verifier 借助密码配对进行验证

保证参数的生成者不泄密 ——> 多方的 Setup

至此，一个用来证明多项式知识的完整的 zk-SNARK 协议就构造出来了，不过现在的协议在通用性上依然还有很多限制，后面的文章将继续介绍如何构造通用的 zk-SNARK。

原文链接

https://arxiv.org/pdf/1906.07221.pdf

https://medium.com/@imolfar/why-and-how-zk-snark-works-2-proving-knowledge-of-a-polynomial-f817760e2805

https://medium.com/@imolfar/why-and-how-zk-snark-works-3-non-interactivity-distributed-setup-c0310c0e5d1c

参考文献

[Dam91] — Ivan Damg ård. “Towards practical public key systems secure against chosen ciphertext attacks”. In: Annual International Cryptology Conference. Springer. 1991, pp. 445–456.

[Gro10] — Jens Groth. “Short pairing-based non-interactive zero-knowledge arguments”. In: International Conference on the Theory and Application of Cryptology and Information Security. Springer. 2010, pp. 321–340.

[JSI96] — Markus Jakobsson, Kazue Sako, and Russell Impagliazzo. “Designated verifier proofs and their applications”. In: International Conference on the Theory and Applications of Cryptographic Techniques. Springer. 1996, pp. 143–154.

[DBS04] — Ratna Dutta, Rana Barua, and Palash Sarkar. Pairing-Based Cryptographic Protocols: A Survey. Cryptology ePrint Archive, Report 2004/064. https://eprint.iacr.org/2004/064. 2004.

[DK18] — Apoorvaa Deshpande and Yael Kalai. Proofs of Ignorance and Applications to 2-Message Witness Hiding. Cryptology ePrint Archive, Report 2018/896. https://eprint.iacr.org/2018/896. 2018.

[Wil16] — Zooko Wilcox. The Design of the Ceremony. 2016. url: https://z.cash/blog/the-design-of-the-ceremony/

作者：Maksym Petkus

翻译 & 注解：even@安比实验室（even@secbit.io）

校对：valuka@安比实验室

本系列文章已获作者中文翻译授权。