测试文章搬家发布
- Tiny熊
- 更新于 2023-11-03 10:40
- 阅读 25
编译:DODOResearch作者:0xAlphaCo-founder@DeriProtocol欢迎关注推特:@0x_Alpha0xAlpha投稿DODOresearch。这篇文章将用数学解码这项技术,揭示它如何在不透露任何信息的情况下证明知识的真实性。准备好,让我们一起揭开
编译:DODO Research
作者:0xAlpha Co-founder @DeriProtocol
欢迎关注推特:@0x_Alpha

0xAlpha 投稿 DODO research。这篇文章将用数学解码这项技术,揭示它如何在不透露任何信息的情况下证明知识的真实性。准备好,让我们一起揭开 zk-SNARK 的神秘面纱。
介绍
zk-SNARK,即“零知识简洁非交互式知识论证”,使得一名验证者 能够确认一名证明者 拥有某些特定知识,这些知识被称为 witness,满足特定的关系,而无需透露关于见证本身的任何信息。
为特定问题生成 zk-SNARK 包括以下四个阶段:1. 将问题(或函数)转换成算术门电路。
- 然后将这个电路翻译成矩阵公式。
- 这个矩阵公式进一步转换成一个多项式,这个多项式应该能被一个特定的最小多项式整除。
- 最后,这种可整除性在有限域的椭圆曲线点中表示出来,证明就在这里进行。
前三个步骤仅仅是转换了原始陈述的表示方式。最后一个步骤使用同态加密将第三步的陈述投影到加密空间中,使得证明者能够证实其中的镜像陈述。鉴于这种投影利用了非对称加密,从第三步的陈述回溯到原始陈述是不可行的,确保了零知识的暴露。
阅读本文所需的数学背景相当于 STEM 专业学生的大一级代数水平。唯一可能具有挑战性的概念可能是椭圆曲线加密。对于不熟悉这一点的人来说,可以将其视为具有特殊基数的指数函数,同时要记住其逆函数仍然未解。
本文将遵循以下符号规则:- 矩阵:粗体大写字母,例如 ;显式形式写作
- 向量:带箭头的小写字母,例如;显式形式写作 ;默认情况下所有向量均为列向量
- 标量:常规字母表示
让我们用这个问题作为例子:
$$ \begin{equation} f(x)=x^3+x^2+5 \end{equation} $$
假设爱丽丝想要证明她知道一个。我们将逐步介绍爱丽丝为她的证明生成 zk-SNARK 所需采取的整个程序。
这个问题可能看起来太简单,因为它不涉及控制流(例如,if-then-else)。然而,将带有控制流的函数转换为算术表达式并不困难。例如,让我们考虑以下问题(或在编程语言中的“函数”):
f(x, z):
if(z==1):
return x*x*x+x*x+5
else:
return x*x+5将这个问题重写为以下算术表达式很容易(假设 ),这并不比方程式 (1) 复杂多少。
$$ f(x,z)=(z-1)(x^2+5)+z(x^3+x^2+5)
$$
在本文中,我们将继续使用方程式 (1) 作为讨论的基础。
第1步:算术门电路
方程式 (1) 可以分解为以下基本算术运算:
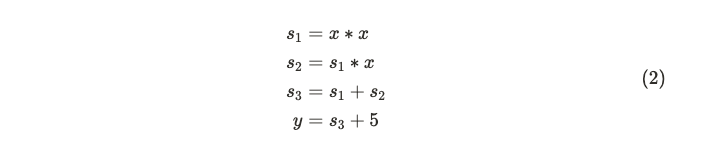
这对应于以下算术门电路:
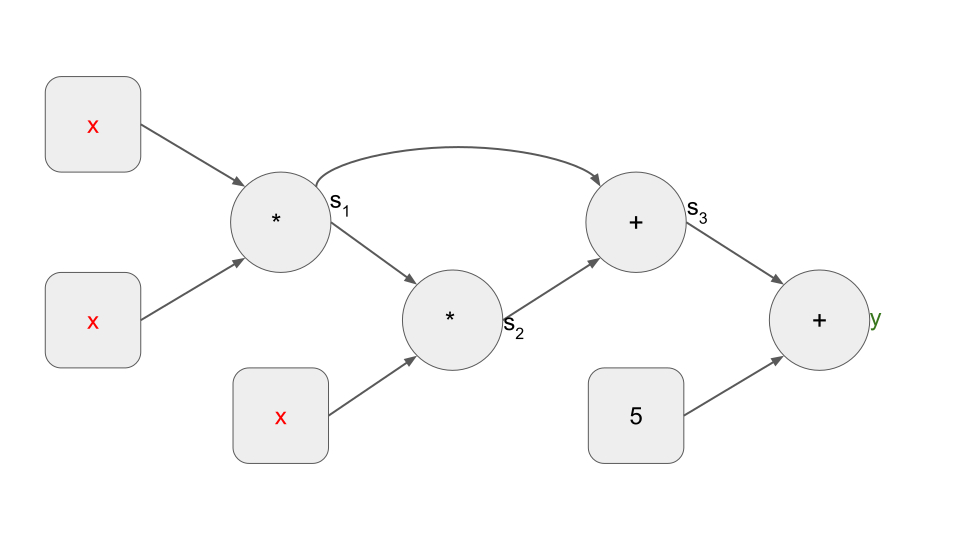 我们还将方程式 (2) 称为一组4个“一级约束”,每个约束描述了电路中一个算术门的关系。通常,一组 n 个一级约束可以概括为一个二次算术程序(QAP),接下来将进行解释。
我们还将方程式 (2) 称为一组4个“一级约束”,每个约束描述了电路中一个算术门的关系。通常,一组 n 个一级约束可以概括为一个二次算术程序(QAP),接下来将进行解释。
第2步:矩阵
首先,让我们定义一个“见证”向量,如下所示:
$$ \vec s=\begin{bmatrix} 1\ x\ y\ s_1\ s_2\ s_3\ \end{bmatrix} =\begin{bmatrix} 1\ x\ s_3+5\ x\cdot x\ s_1\cdot x\ s_1+s_2\ \end{bmatrix} $$
其中 与方程式 (2) 中定义的相同。
通常,对于一个有 个输入和 个算术门的问题(即 n-1 个中间步骤和最终输出),这个见证向量将是 维的。在实际问题中,数字 可能非常大。例如,对于哈希函数, 通常是几千。
接下来,让我们构造三个 n(m+n+1) 矩阵 ,以便我们可以将方程式 (2) 重写如下:
$$ \begin{equation} \boldsymbol A\vec s \odot\boldsymbol B\vec s=\boldsymbol C\vec s \end{equation} $$
其中表示逐点乘积,而且
$$ \boldsymbol A=\begin{bmatrix} \vec a_1^T\ \vec a_2^T\ \vec a_3^T\ \vec a_4^T\ \end{bmatrix}=\begin{bmatrix} 0, 1, 0, 0, 0, 0\ 0, 0, 0, 1, 0, 0\ 0, 0, 0, 1, 1, 0\ 5, 0, 0, 0, 0, 1\ \end{bmatrix}, \ $$
$$ \boldsymbol B=\begin{bmatrix} \vec b_1^T\ \vec b_2^T\ \vec b_3^T\ \vec b_4^T\ \end{bmatrix}=\begin{bmatrix} 0, 1, 0, 0, 0, 0\ 0, 1, 0, 0, 0, 0\ 1, 0, 0, 0, 0, 0\ 1, 0, 0, 0, 0, 0\ \end{bmatrix}, \ $$
$$ \boldsymbol C=\begin{bmatrix} \vec c_1^T\ \vec c_2^T\ \vec c_3^T\ \vec c_4^T\ \end{bmatrix}=\begin{bmatrix} 0, 0, 0, 1, 0, 0\ 0, 0, 0, 0, 1, 0\ 0, 0, 0, 0, 0, 1\ 0, 0, 1, 0, 0, 0\ \end{bmatrix}. $$
方程式 (3) 只是方程式 (2) 的另一种表示形式:每组 对应于电路中的一个门。我们只需要明确地展开矩阵公式就可以看到这一点:
$$ \text{LHS} =\begin{bmatrix} 0, 1, 0, 0, 0, 0\ 0, 0, 0, 1, 0, 0\ 0, 0, 0, 1, 1, 0\ 5, 0, 0, 0, 0, 1\ \end{bmatrix}\begin{bmatrix} 1\ x\ y\ s_1\ s_2\ s_3\ \end{bmatrix}\odot \begin{bmatrix} 0, 1, 0, 0, 0, 0\ 0, 1, 0, 0, 0, 0\ 1, 0, 0, 0, 0, 0\ 1, 0, 0, 0, 0, 0\ \end{bmatrix}\begin{bmatrix} 1\ x\ y\ s_1\ s_2\ s_3\ \end{bmatrix}
\begin{bmatrix} x\ s_1\ s_1+s_2\ s_3+5\ \end{bmatrix} \odot \begin{bmatrix} x\ x\ 1\ 1\ \end{bmatrix} \= \begin{bmatrix} x\cdot x\ s_1\cdot x\ s_1+s_2\ s_3+5\ \end{bmatrix} $$
$$ RHS= \begin{bmatrix} 0, 0, 0, 1, 0, 0\ 0, 0, 0, 0, 1, 0\ 0, 0, 0, 0, 0, 1\ 0, 0, 1, 0, 0, 0\ \end{bmatrix} \begin{bmatrix} 1\ x\ y\ s_1\ s_2\ s_3\ \end{bmatrix}
\begin{bmatrix} s_1\ s_2\ s_3\ y \end{bmatrix} $$
所以 与方程式 (2) 完全相同,矩阵方程的每一行对应一个一级约束(即电路中的一个算术门)。
我们跳过了构建 的步骤,其实这些步骤相对简单直接。我们只需要根据相应的一级约束,把它们转换成矩阵形式,从而确定 每一行的内容,即 。以第一行为例:可以很容易地看出,要使第一个一级约束 成立,我们需要的是将 、 和 与 相乘。
因此,我们已经成功地把算术门电路转换成了矩阵公式,即方程式 (3)。同时,我们也把需要证明掌握的对象,从 转变为了见证向量 。
第3步:多项式
现在,让我们构造一个 n(n+m+*1) 矩阵 ,它定义了一组关于 的多项式:
$$ \vec p_A(z)=\boldsymbol P_A^T\begin{bmatrix} 1\z\z^2\z^3 \end{bmatrix} $$
使得在 {1,2,3,4}处的取值满足以下条件:
$$ \vec p_A(1)=\vec a_1^T, \ $$
$$ \vec p_A(2)=\vec a_2^T, \ $$
$$ \vec p_A(3)=\vec a_3^T, \ $$
$$ \vec p_A(4)=\vec a_4^T. $$
然后我们可以将重写为:
$$ \boldsymbol A=\begin{bmatrix}\vec a_1^T\ \vec a_2^T\ \vec a_3^T\ \vec a_4^T\end{bmatrix}
\begin{bmatrix} \begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=1}\ \begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=2}\ \begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=3}\ \begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=4}\ \end{bmatrix} $$
这些是六个变量的四组线性方程,可以用传统方法求解。然而,在这种情况下解决 的更有效方法是拉格朗日插值,它利用了问题的特殊性。这里我们跳过求解 的过程,虽然有点繁琐但很直接。
类似地,我们分别为 和 构造 和 。然后我们可以将矩阵公式 重写为:
$$ \begin{bmatrix}\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=1}\\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=2}\\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=3}\\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=4}\\end{bmatrix}\vec s \odot \begin{bmatrix}\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PB|{z=1}\\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PB|{z=2}\\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PB|{z=3}\\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PB|{z=4}\\end{bmatrix}\vec s
\begin{bmatrix}\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PC|{z=1}\\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PC|{z=2}\\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PC|{z=3}\\begin{bmatrix}1,z,z^2,z^3\end{bmatrix}\boldsymbol PC|{z=4}\\end{bmatrix}\vec s $$
如果提取出每一行单独观察,不难发现这四行对应于在四个点分别求值的相同表达式。因此,上述矩阵方程等价于:
$$ P(z)= 0, \text{at z=1,2,3,4} $$
其中定义为:
$$ P(z)=\begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol P_A\vec s \cdot \begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol P_B\vec s - \begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol P_C\vec s $$
确定 在 是否成立的最快方法是检查它是否可以被 整除,这被称为“最小多项式”,记为 。即检查 的因式分解:是否存在一个多项式 使得 可以分解为 。换句话说,我们需要证明以下分解:
$$ \begin{equation} p_A(z)\times p_B(z)-p_C(z)=h(z)\times t(z) \end{equation} $$
其中:
$$ p_A(z)=\begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol P_A\vec s, $$
$$ p_B(z)=\begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol P_B\vec s,\ $$
$$ p_C(z)=\begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol P_C\vec s. $$
一种直接但不保密的方式来证明这一点是提供方程式 (4) 的左边并展示因式分解。然而,zk-SNARK 的主要目的是保持隐秘(不透露任何知识)。因此,我们不会直接证明这个方程,而是在椭圆曲线点的空间中证明它的加密版本。
第4步:椭圆曲线点
将方程式 (4) 重写为:
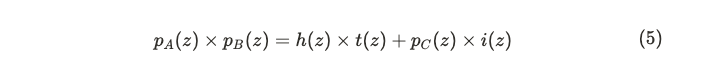
其中 只是 的一个平凡的零次多项式,用来使方程统一——所有项都是二次的。这样做的必要性很快就会变得清晰。注意这个方程只包含 的多项式的加法和乘法。
从高层次上看,这就是我们要做的:将多项式(具体来说,是多项式的系数)映射到椭圆曲线点,并将方程式 (5) 转换为加密空间中的以下镜像方程,这是需要证明的陈述:
$$ E(p_A)\otimes E(p_B) = E(h)\otimes E(t) \oplus E(p_C)\otimes E(1) $$
请注意,算术运算,加法 和乘法 ,也被映射到椭圆曲线点的有限域上的对应运算。圆圈中的运算符号 和 用来避免混淆,并表明这些是重新定义的域运算。
接下来,我们将更详细地阐述实际的操作步骤。
椭圆曲线加密
椭圆曲线的一般理论远远超出了本文的范围。就本文的目的而言,椭圆曲线被定义为从素域 的函数,其中 包括满足 的点(称为椭圆曲线点,简称 ECPs)。
请注意,虽然到目前为止我们一直在讨论常规算术,但现在当我们转换到素域时,数字的算术运算是以模运算的方式进行的。例如,,其中 是 的阶。
另一方面,两个椭圆曲线点的加法定义如下图所示:
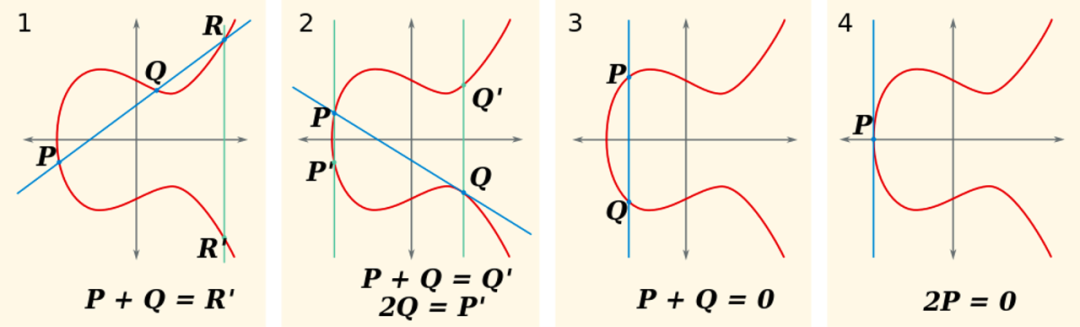
Figure from Wikipedia
具体来说,两个 ECPs和的加法:1. 找到直线 和曲线的交点 ,定义为
- 翻转到曲线上 的“镜像”点 。
因此我们定义椭圆曲线点的加法:
请注意,这个规则也适用于特殊情况,即一个 ECP 自加的情况,此时将使用该点的切线。
现在假设我们随机选择一个点 ,并将数字 映射到它上面。(这种“初始映射”听起来有点任意。稍后将进行讨论)。然后对于任何 ,我们定义:
$$ E(n):= G\oplus G\oplus ...\oplus G = G\cdot n $$
这有一个操作表达式。定义 的操作为“生成器”,记为 。那么上述定义等同于:
$$ E(n):= g^n $$
也就是说, 是从 开始,进行 次 操作的椭圆曲线点。这实际上是椭圆曲线加密最初构建的方式:1. 从 作为 开始;
- 然后进行 操作跳转到 :曲线和 处切线的交点的翻转;
- 然后再次进行 操作跳转到 :曲线和直线 的交点的翻转;
- 依此类推。
所以 操作就像 中的 “++” 操作符。(请记住, 中的加法是以模运算的方式定义的)。
对于不熟悉椭圆曲线的人来说,你可以将这种映射类比为一个常规的指数函数,其中基数 代替了实数。算术运算的行为类似。然而,一个关键的区别是 的逆函数在计算上是不可行的。也就是说,没有办法计算椭圆曲线版本的 。这当然是椭圆曲线加密的基础。这样的映射被称为单向加密。
请注意,给定一个椭圆曲线,由于选择 (因此选择“生成器” )是任意的(除了 x 轴上的点),有无限种映射方式。选择 (或 )可以类比为选择指数函数的基数(),这是常识的一部分。
定义了加法后,以下线性关系很容易看出:
$$ E(n+m)=G\cdot(n+m)=G\cdot n\oplus G\cdot m=E(n)\oplus E(m) $$
范数表达:
$$ g^{n+m}=g^ng^m=g^n\oplus g^m $$
因此, 中的任何线性关系(或约束)都会通过这种映射在加密空间 中得到保留。例如, 中的方程 将导致 ,或者 。
然而,Alice 想要证明的方程式 (5) 是二次形式的,所以线性不够。为了处理二次项,我们需要在加密空间中定义乘法。这被称为配对函数,或双线性映射,接下来将进行解释。
双线性映射
假设 和 是素数阶 的群。配对函数,或 双线性映射,定义为:
$$ e:G_1\times G_2\mapsto G_T $$
使得如果 分别是 和 的生成器,则 是 的生成器,并且 。
这个配对函数是我们在加密空间中需要的“乘法”操作,用于处理方程式 (5) 中的二次项。
$$ e(A, B\oplus C)=e(g^a, h^bh^c)=e(g^a, h^b)e(g^a, h^c)=e(A,B)\oplus e(A,C)\ $$
$$ e(A\oplus D, C)=e(g^ag^d, h^c)=e(g^a, h^c)e(g^d, h^c)=e(A,B)\oplus e(D,C)
$$
其中是和中的元素。这个定义当然比本文所需的更为一般。你可以把看作是椭圆曲线点。
让我们用作为乘法操作的符号,那么双线性可以用算术形式重写:
$$
A\otimes(B\oplus C)=(A\otimes B)\oplus(A\otimes C)\ $$
$$ (A\oplus B)\otimes C=(A\otimes B)\oplus(B\otimes C) $$
这是我们都熟悉的东西——加法和乘法操作的分配律。
有了这样的双线性映射,我们就可以将方程式 (5) 的两边映射到加密空间。### 公共参考字符串
在这里,我们需要一个可信的第三方来选择五个随机系数:,以及一个随机点 ,在这个点上将会(虚拟地)评估多项式。这个 6 元组 被称为“toxic waste”,需要被丢弃。
请注意,整个程序基于对第三方正确处理有毒数据的信任。在现实中,这个“可信设置”程序并不是一个简单的任务。在这篇文章中,我们将假设这一步骤将被正确进行。
设 ,并计算:-
这整体被称为“证明钥”(proving key),记为 PK。请注意, 中包含向量的表示法应该被解释为椭圆曲线点的向量,其中每个点都是从相应的向量元素映射而来的。所以这 11 个向量实际上包含 62(=42+63+63+63)个椭圆曲线点。这 62 个 ECP 将被提供给 Alice,即证明者。在一个一般的情况下,对于一个有 个输入和 个一级约束的问题,PK 将包含 个 ECP。
同时,进行以下计算:-
整个过程被称作“验证钥”,简称VK。这里只涉及7个椭圆曲线点(ECPs),需要提供给验证方。要注意的是,不管问题里面涉及多少输入和一级约束,VK始终是由7个ECPs构成的。
另外,值得一提的是,“可信设置”以及生成PK和VK的过程,对于一个特定的问题来说,只需操作一次即可。### 证明与验证
现在拥有公钥(PK),爱丽丝将计算以下椭圆曲线点(ECPs):
- $E_\beta=E(\beta_A\vec z_0 \boldsymbol P_A \vec s+\beta_B\vec z_0 \boldsymbol P_B \vec s+\beta_C\vec z_0 \boldsymbol P_C \vec s)=E(\beta_A\vec z_0 \boldsymbol P_A)\vec s+E(\beta_B\vec z_0 \boldsymbol P_B)\vec s+E\beta_C\vec z_0 \boldsymbol P_C)\vec s)$
这9个椭圆曲线点就是零知识简洁非交互式证明(zk-SNARK)的关键!
注意,爱丽丝其实只是对公钥里的椭圆曲线点做了些线性组合运算。这点特别关键,验证时会重点检查。
现在,爱丽丝交出了zk-SNARK证明,咱们终于进入验证环节,分三步走。
首先得确认,前8个椭圆曲线点真的是通用参考串里那些点的线性组合。
$$ E_A\otimes E(\alpha)=E_A'\otimes E(1)\ $$
$$ E_B\otimes E(\alpha)=E_B'\otimes E(1)\ $$
$$ E_C\otimes E(\alpha)=E_C'\otimes E(1)\ $$
$$ E_h\otimes E(\alpha)=E_h'\otimes E(1)\ $$
其次,检查确实来自同一个见证向量:
$$ E_\beta\otimes E(\gamma)= E_A\otimes E(\gamma\beta_A)\oplus E_B\otimes E(\gamma\beta_B)\oplus E_C\otimes E(\gamma\beta_C) $$
最后,检查等式(5)的相等性:
$$ E_A\otimes E_B=E_h\otimes E_t\oplus E_C\otimes E(1) $$
如果这三项检查都成立,那么等式(5)得到验证,因此我们相信爱丽丝知道见证。
让我们解释一下等式背后的理由。以第一部分中的第一个等式为例,等式成立是因为双线性性质:
$$ E_A\otimes(E(1)\cdot \alpha) =(E(A)\cdot \alpha) \otimes E(1) $$
然而,由于爱丽丝不知道 的值,她无法明确计算这个加法。她唯一能想出来满足等式的一对 的方法,是分别用相同的一组系数 ,计算 和 的两个组合。###
参考文献1. “Zk-SNARKs: Under the Hood” (Vitalik Buterin)
- “A Review of Zero Knowledge Proofs” (Thomas Chen, Abby Lu, Jern Kunpittaya, and Alan Luo)
- “Why and How zk-SNARK Works: Definitive Explanation” (Maksym Petkus)
- Website: Zero-Knowledge Proofs
- Wikipedia: Elliptic curve
- Wikipedia: Finite field
- Wikipedia: Pairing-based cryptography
免责声明
本研究报告内的信息均来自公开披露资料,且本文中的观点仅作为研究目的,并不代表任何投资意见。报告中出具的观点和预测仅为出具日的分析和判断,不具备永久有效性。
推荐阅读
01
浴火重生的 Solana 生态 - Jito Network 介绍 | CryptoSnap
02
03
关于我们
「DODO Research」是一个专业的 Web3 研究机构,由一群对 Crypto 有信仰和热情的研究者组成,我们持续关注追踪 Web3 中的 DeFi 和基础设施等相关赛道,提供深入的见解和观点。
欢迎大家 DM ,分享任何关于 DeFi 和 Web3 基础设施的见解和想法,或是你希望了解的深度话题。
另外我们也在寻找志同道合的小伙伴,欢迎同样有热情的你加入我们,在这你能与最懂 DeFi 的小伙伴一起探索精彩的 Web3 世界。
请联系我们:邮箱:dodoingresearch@gmail.com
我们在招聘的岗位有:
1)DeFi / Web3基础设施 研究员
2)品牌运营
具体招聘需求传送:https://twitter.com/DodoResearch/status/1587274217082404864
我们的研究内容会同步发布在Twitter,Notion和Mirror上,欢迎关注:
Twitter: https://twitter.com/DodoResearch;
Notion: https://dodotopia.notion.site/Dr-DODO-is-Researching-6c18bbca8ea0465ab94a61ff5d2d7682;
Mirror:https://mirror.xyz/0x70562F91075eea0f87728733b4bbe00F7e779788
- 测试文章长度---11 25 浏览
- 测试文章长度---11 23 浏览
- 测试文章长度---10 23 浏览
- 测试文章长度---4 25 浏览
- 文章发布测试7 25 浏览
- 测试文章发布6 25 浏览
- 文章发布测试4 23 浏览
- 运行 v0.7 及更早版本的 Bitcoin Core 25 浏览
- 测试空投--2 28 浏览
- 测试自动空投 30 浏览
- 測試自動空頭 26 浏览
- 创建文章--测试nft空投 22 浏览
