区块链中的数学 -- MultiSet check& Schwartz–Zippel lemma
- blocksight
- 发布于 2021-06-26 11:04
- 阅读 495
本文介绍的这些知识点是理解plookup的基础
写在前面
上一篇介绍了环签名技术,环签名是群签名的一种,关于群签名,感兴趣可以自行查阅,了解更多!
我们之前有一系列的文章和视频围绕plonk的算法和工程代码,有些视频没有总结为文字blog,如果你感兴趣,我们欢迎你在看完视频后,整理出相应文字版本,“纸上得来终觉浅,绝知此事要躬行”,临渊羡鱼(听别人说)和退而结网(自己去做)是两个层面的事情,将自己的理解 --> 总结--> 讨论 --> 提高,结识志同道合的朋友,是我们一贯提倡并坚持的方法。
感兴趣的欢迎留言! 本文将介绍plonk中重要的一个优化方向---plookup思路!理解本文的最好了解plonk相关技术及术语。
多集合检验(Multiset checks )
多集合检验的问题是: 假如有两个集合$a = {a_1,...,a_n}$, $b = {b_1,...,b_n}$,如何检验a,b集合相同,即元素相同。 直接的做法是循环比较,显然效率不高。引入plonk permutation的思路,采用“grand product reduction”,具体为:
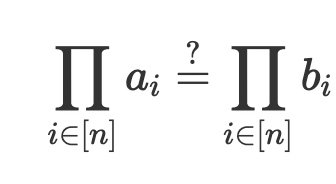
如果a,b相等,那么各自元素的乘积也必然相等。反之呢,不一定!考虑a = {3, 4}, b= {2. 6}例子。 我们还需引入Schwartz–Zippel来解决这个问题。
Schwartz–Zippel lemma: 对于域F内的d次多项式f(x)。随机给x 赋值为F中的随机一个元素。为0 的几率为$\frac{d}{F}$,当阶数d远小于域范围时,该概率可以忽略
看起来很简单,比较容易理解,往往越简单力量越大! 接下来往集合中每个元素都加入一个随机项r,
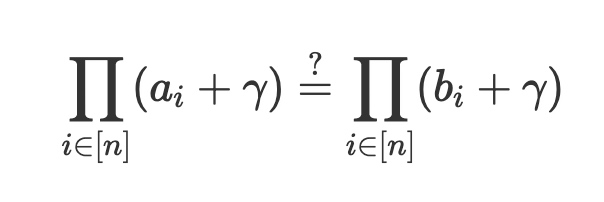
这时候可以说,如果乘积相等,则集合相等,反之也成立。即是充分必要条件。 从Schwartz–Zippel lemma视角来看,等式两边是两个多项式 $fa(x)=\prod^n{i=0}(a_i+x)$,$fb(x)=\prod^n{i=0}(b_i+x)$ 当x随机取值r时, 如果 $f_a(r)=f_b(b)$,则$f_a(x)=f_b(x)$
这里隐式地将集合(或者称为向量vector)转化成多项式函数。我们认为二者一定范围内等同,零知识证明中大量使用多项式术语(多项式函数,承诺等),很多初学朋友问为什么要搞成多项式? 因为多项式可以实现简洁的验证,zksnark中s(Succinct)主要通过这种方式来实现,通过上面简单的例子可以窥探一二,如果你有不同理解,欢迎讨论!
关于Schwartz–Zippel lemma的更多应用,理解randomize的力量,值得慢慢体会,更多地可查阅本文参考资料。
plonk Permutation
Permutation这个思路,算法视频中已经讲得很清楚了。这里从Multiset checks角度来看, Permutation σ: [n]-->[n] ,a, b集合都有n个元素,检验满足$b_i=a_σ(i)$, 即下面两个集合相等:
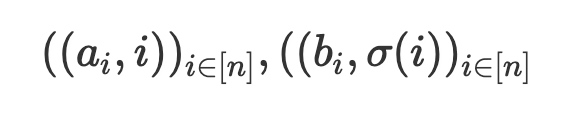
这是多元集合校验,把它约化成单项元素,然后可以使用多集合检验的方法了。 随机选择β,构造如下两个单元项集合:
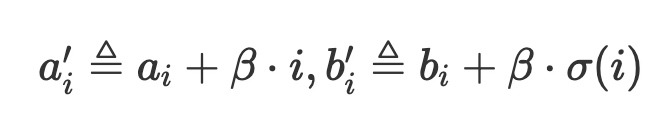
对a', b'可直接使用Multiset checks方法了。 相关plonk系列视频
小结
本文介绍的这些知识点是理解plookup的基础,脚踏实地才能仰望星空,下一篇将继续介绍plookup算法!
参考: Plookup.pdf https://hackmd.io/@arielg/ByFgSDA7D https://en.wikipedia.org/wiki/Schwartz%E2%80%93Zippel_lemma
原文链接:https://mp.weixin.qq.com/s/Yg0Niv2Avf7Toj6rUPZP8Q 欢迎关注公众号:blocksight
相关阅读
区块链中的数学 -盲签名(Blind Signature) 盲签名原理
区块链中的数学 - sigma协议OR Proof&签名 sigma协议的扩展--OR proof
区块链中的数学-sigma协议与Fiat-Shamir变换 sigma协议与Fiat-Shamir变换
区块链中的数学 - 何谓零知识证明? 何谓零知识证明
区块链中的数学 - RSA累加器的非成员证明 RSA Accumulator非成员证明以及区块链应用
区块链中的数学 - Accumulator(累加器) 累加器与RSA Accumulator
区块链中的数学 - Kate承诺batch opening Kate承诺批量证明
区块链中的数学 - 多项式承诺 多项式知识和承诺
区块链中的数学 - Pedersen密钥共享 Pedersen 密钥分享
区块链中的数学 - Pedersen承诺 密码学承诺--Pedersen承诺
区块链中的数学 - 不经意传输 不经意传输协议
区块链中的数学 - RSA算法加解密过程及原理 RSA加解密算法
区块链中的数学 - BLS门限签名 BLS m of n门限签名
区块链中的数学 - BLS密钥聚合 BLS密钥聚合
Schorr 签名基础篇 Schorr签名与椭圆曲线
区块链中的数学-Uniwap自动化做市商核心算法解析 Uniwap核心算法解析(中)
- 华为云社区 96 浏览
- 测试文章 51 浏览
- 一文读懂零知识证明(ZKP) 375 浏览
- 区块链中的数学 - Halo2 Circuit 349 浏览
- 零知识证明 - zkEVM解读 356 浏览
- ZKopru:结合 ZKP 和 Optimistic Rollup 271 浏览
- Dark Forest - 采用零知识证明技术的游戏 437 浏览
- zkEVM - Hermez设计思路 304 浏览
- 零知识证明 - Plookup算法介绍 340 浏览
- Tornado.cash: 一个关于匿名和zk-SNARKs的故事 445 浏览
- 简明理解零知识证明历史、原理与发展现状 451 浏览
- 区块链中的数学--PLookup 559 浏览
