uniswap - V3技术白皮书导读
- Star Li
- 发布于 2021-04-08 15:36
- 阅读 4883
uniswap V3版本核心思想是流动性集中。流动性提供者可以在某个区间提供流动性,提高资金使用率。在某个区间获取的交易费,由所有在该区间的流动性提供者均分。uniswap V3设计了区间粒度-Tick,并且推导了流动性添加/删除以及费用计算的过程。在之基础上,uniswap V3也更新了价格预言机的实现。
uniswap V3一公布就引发广泛关注。相对V2来说,逻辑和代码都复杂一些。V3的核心是通过盘口区间提供流动性(集中式流动性),解决LP提供流动性时的资金利用率的问题。什么是资金利用率?V3如何推导区间流动性的计算公式?如何理解流动性?如何计算swap费用?本文先从V3技术白皮书详细分析开始。
先给出一些uniswap官方有关V3的资料:
- V3官方介绍
https://uniswap.org/blog/uniswap-v3/
- 技术白皮书
https://uniswap.org/whitepaper-v3.pdf
- 智能合约代码
https://github.com/Uniswap/uniswap-v3-core
https://github.com/Uniswap/uniswap-v3-periphery
推荐先认真查看技术白皮书,再看智能合约代码,最后再对照官方介绍。理解了技术白皮书,代码非常容易理解。在技术白皮书的第一章总结了uniswap V3的技术特点,最核心的概念是"Concentrated Liquidity" (集中式流动性)。
1 资金利用率
先看看uniswap V2的资金利用率:
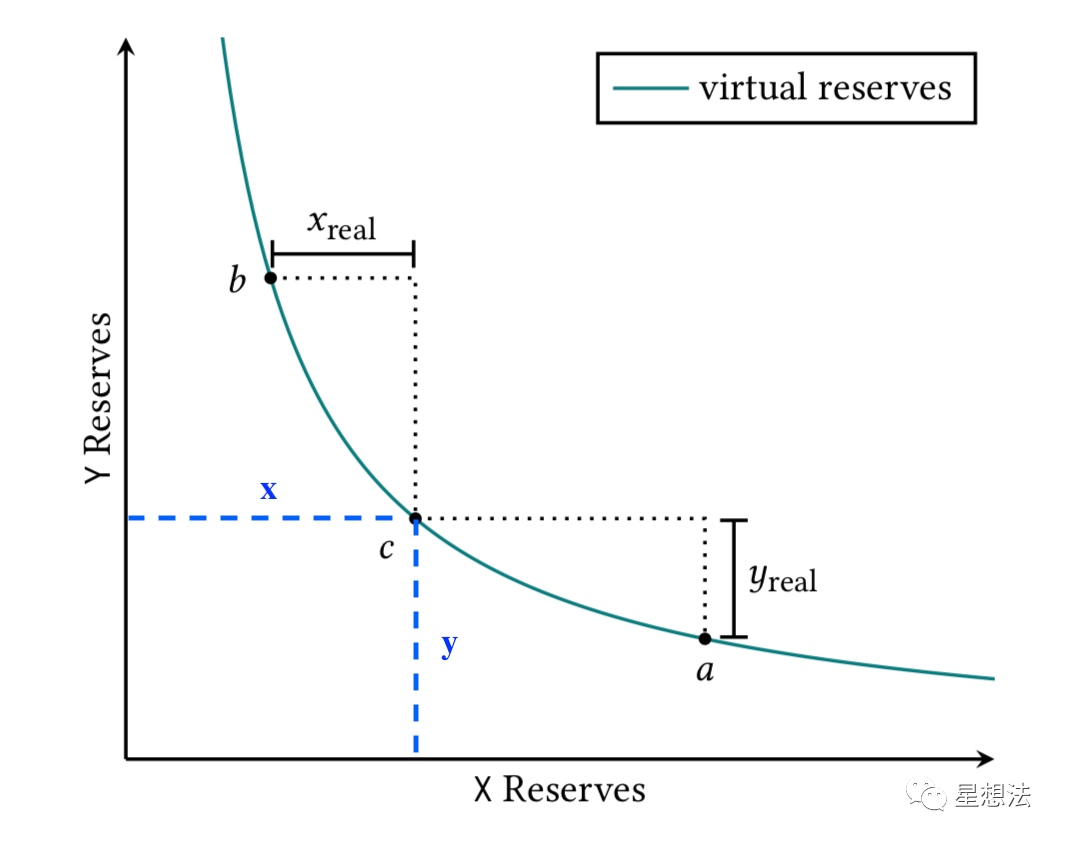
上图为资金池中的x/y的量变化曲线。资金池中的当前价格在c点,并且假设会在a价格点和b价格点之间波动。从c点向a点滑动,消耗最大y_real,从c点向b点滑动,消耗最大为x_real。也就是说,当前价格c点,在a点和b点之间震荡的话,最大只需要消耗x_real和y_real。理论上只要提供x_real和y_real就足够了。而事实上,如上图所示,在价格c点,分别提供了大于x_real和y_real的x和y。明显可以看出,x-x_real和y-y_real的资金在这种情况下是永远用不上的,也就称为闲置资金。
在这种情况下,资金利用率为x_real/x或者y_real/y。如果价格波动非常小的话,资金利用率是非常低的。uniswap V3就是尝试解决资金利用率低的问题。想法比较简单,所有资金可以只添加到某个区间,只添加到有可能价格波动到的区间范围。如何在某个区间添加流动性并提供swap功能是uniswap V3的重点。先从Virtual Reserves说起。
2 虚拟资金池(Virtual Reserves)
uniswap的交易采用的乘积固定模型(x*y=k)。所谓的虚拟资金池(Virtual Reserves),是指还在乘积固定曲线上,只提供某个区间流动性的资金池:
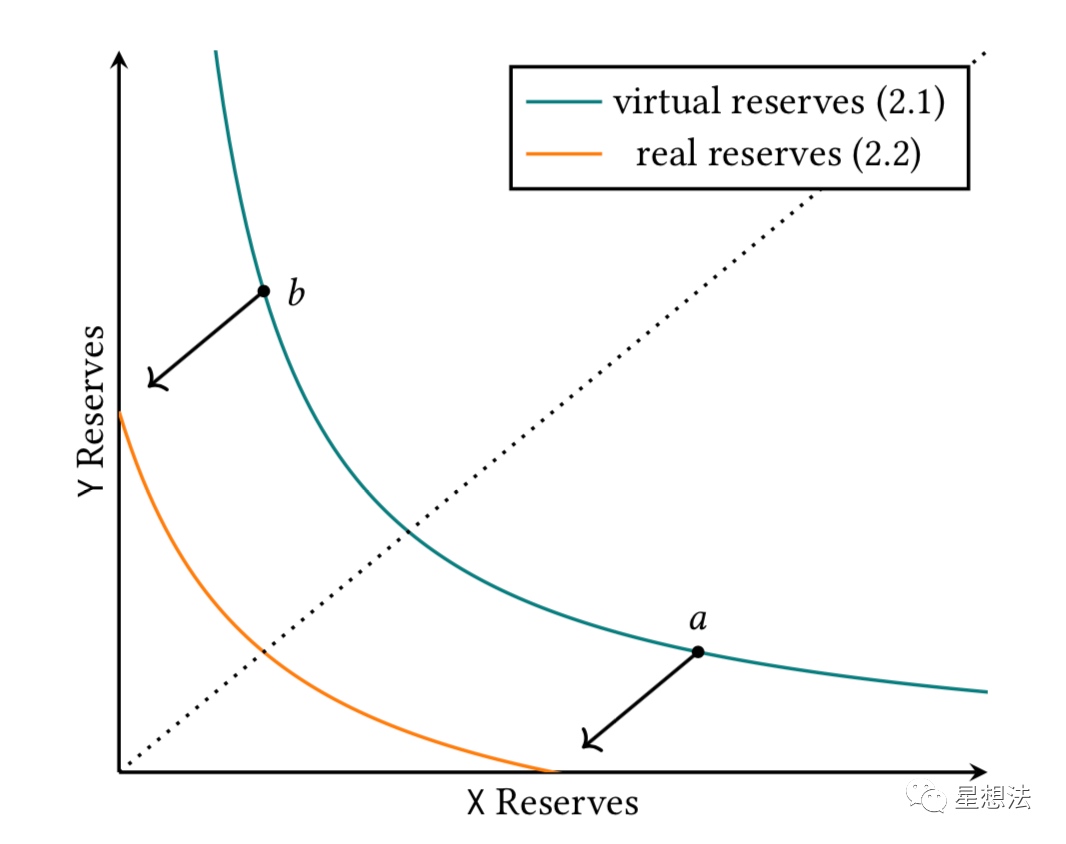
图中的墨绿色的曲线就是虚拟资金池满足的乘积固定曲线。事实上需要的资金的曲线如图中的橘黄色。橘黄色的曲线公式如下图:
$(x+\frac{L}{\sqrt{pb}})(y+L\sqrt{pa})=L^2$
你可以想象成虚拟资金曲线在x/y轴进行平移,使得a/b点和x/y轴重合。也就是用一定量的资金就能达到“虚拟”的交易曲线的效果。
如何计算在某个区间提供虚拟资金池,先要从深入理解流动性开始。
3 流动性(Liquidity - L)
乘积固定的交易模型,满足资金池中的两种代币金额满足:x y = K。如果设定K=L^2的话,x y = L^2。L就是我们说的流动性。由乘积固定的交易模型得出如下的公式:
$L=\sqrt{xy}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6.3)$ $\sqrt P=\sqrt{\frac{y}{x}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6.4)$
在已知L和sqrt(P)的情况下,也能推导出资金需求量x和y。
$x=\frac{L}{\sqrt P}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6.5)$ $y=L \cdot \sqrt P\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6.6)$
通过公式6.6,在流动性不变的情况下(不添加删除流动性),流动性可以看成是单位“价格波动”的y资金量的变化。”价格波动“打上引号是因为事实上是sqrt(P)的变化。
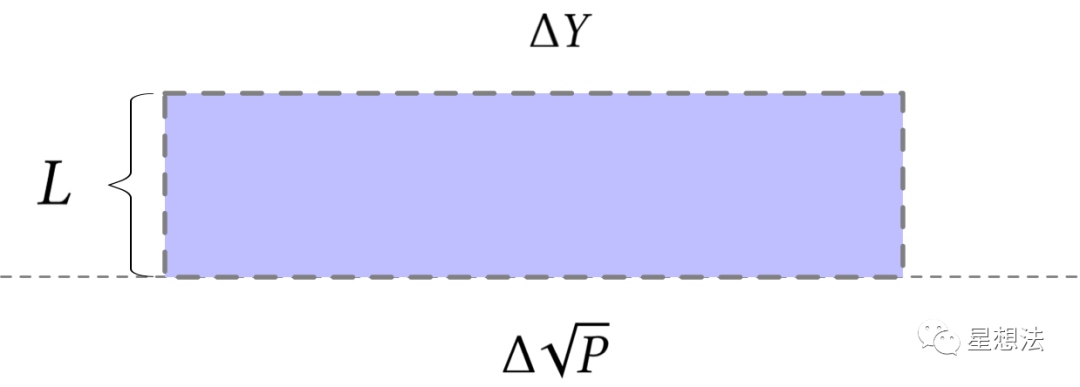
$L=\frac {\Delta Y}{\Delta \sqrt P}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6.7)$
这个是uniswap V3核心公式(6.7),用相对值(资金和价格相对值)来计算流动性。所谓的流动性,就是单位“价格变化”的资金量。在一定的交易量的情况下,如果流动性好,价格变化就小,流动性不够的话,价格波动就大。
特别注意的是,一个区间上的流动性和V2的普适的流动性不同。一个区间上的流动性,重点在“区间上”。不同区间的流动性没有可比性。V2的流动性和区间上的流动性的区别如下图:
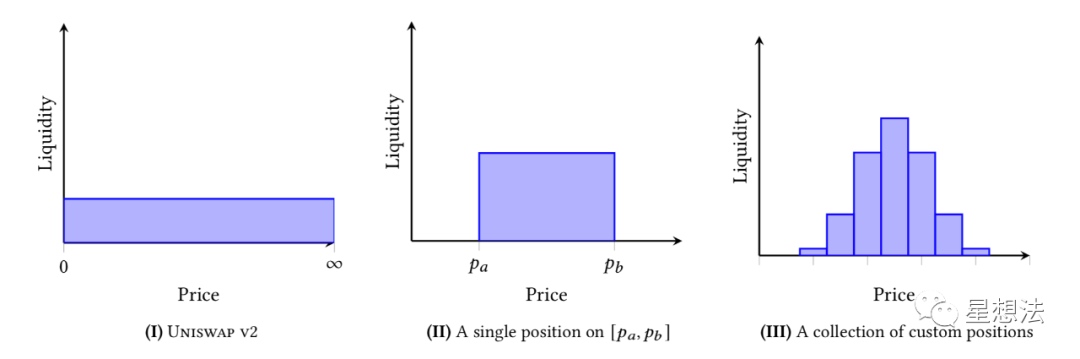
V2的流动性是“普适”的,在所有价格点上流动性相同。V3的流动性是由一系列不同区间上的流动性组成。相对来说,在当前价格左右的流动性比较高。流动性提供者LP只有提供了可供交易的流动性才能获取交易费。为了获取更多的交易费,为了提高资金的利用率,流动性提供者会将资金提供在合理的价格波动范围内。也就是说,在某个区间swap交易产生的手续费,只有该区间流动性提供者才能获取手续费。为了计算每个区间获取的手续费,引入了Tick的概念和计算方法。
4 Tick
在区间上提供流动性,带来很多复杂的情况:区间和区间的重叠覆盖。因为不同区间的流动性没有可比性,某个交易费并不能混入到流动资金中,等删除流动性时候一并提取。为了解决这个问题,uniswap V3引入了Tick的概念。交易费用实时结算并单独记录,并不混入流动资金中。虽然整个区间和区间的流动性没有可比性,但是,在具体的某个价格点上(一个价格片上),流动性是可比较的。uniswap V3将整个价格范围(负无穷到正无穷)分成一个个的Tick(价格点):
$p(i)=1.0001^i\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6.1)$
后一个价格点的价格是前一个价格点价格基础上浮动万分之一。
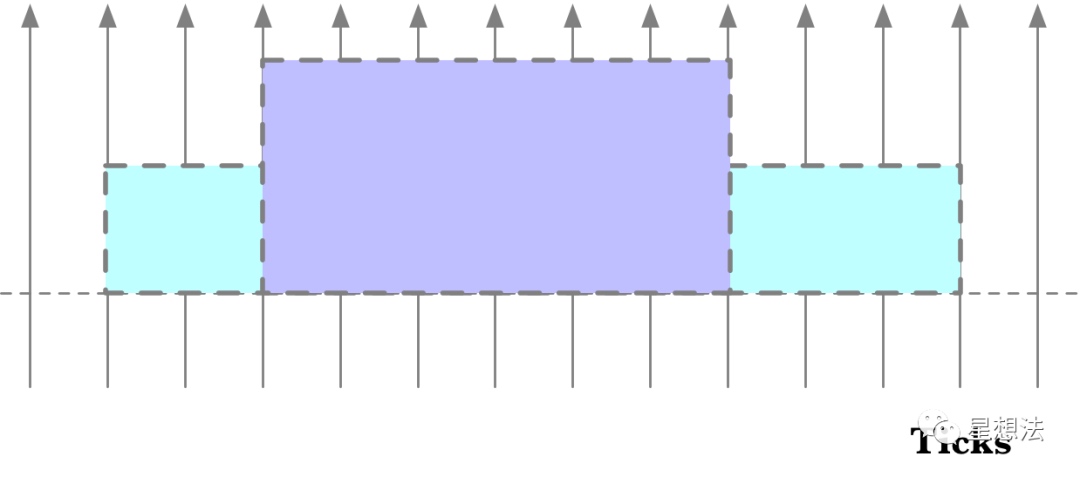
每个Tick也有一个唯一的序号。区间(Position)可以由两个Tick表示。逻辑上交易手续费可以一个个的Tick计算,并在每一个Tick上根据流动性的占比进行交易分配。先看看一个Tick范围的swap的计算。
5 Tick内的SWAP
假设有一个很小的量的y,需要swap为x。通过6.13的公式,可以计算出因为y的变化导致的价格变化。 $\Delta \sqrt P=\frac{\Delta y}{L}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6.13)$
再利用6.15的公式可以算出换取的x的量。
$\Delta \frac{1}{\sqrt P}=\frac{\Delta x}{L}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6.15)$
uniswap V3针对同样的交易对设置了不同的交易费:0.05%,0.3%以及1% (还可以添加其他费率)。如果是从Y换取X,则在换取之前先扣除手续费再进行上述的交换。
在同一交易池中只支持一种费率。也就是说,在一个交易池中支持不同的价格区间,但是都是同样的费率。如果需要添加同样交易对的不同交易费的交易池,必须创建新的交易池。
接下来,深入讲解一下 添加/删除流动性以及交易费用的计算逻辑。
6 添加/删除流动性
V3的添加/删除流动性是当前价格情况下在某个区间添加或者删除流动性。所有的流动性添加/删除流动性采用如下的公式:
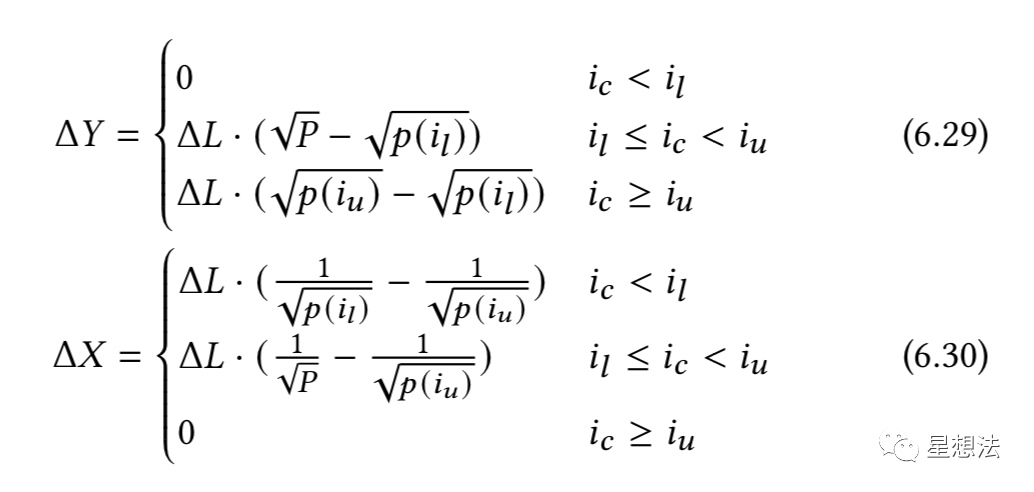
注意,价格变化并不是指区间的大小,而是在某个区间上提供流动性,相对当前价格,“需要相应资金变化”对应的价格变化。
分为三种情况,想要添加的流动性区间和当前价格的关系。
- 当前价格处于流动性价格区间 (il <= ic < iu)
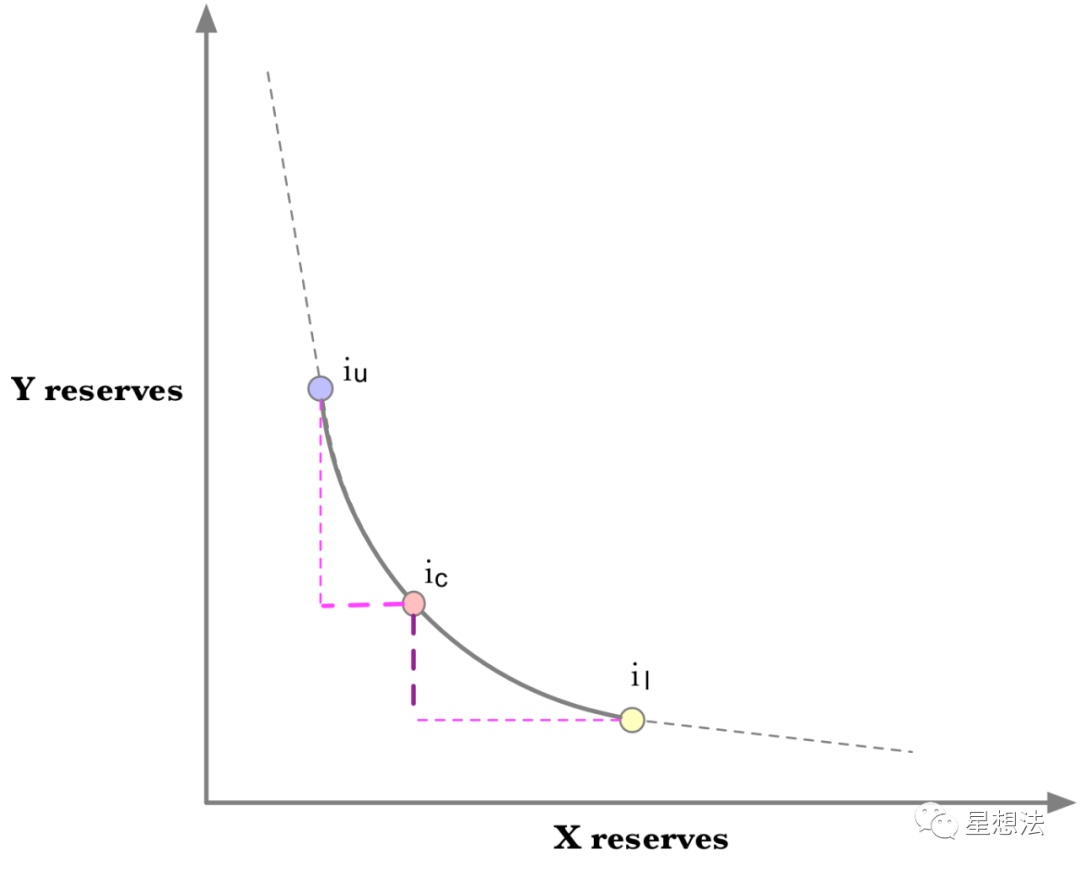
因为价格在区间范围内,如果价格滑动到il,则需要提供y资金。如果价格滑动到iu,则需要提供相应的x资金。所以,对于delta_Y来说的,价格变化为sqrt(P) - sqrt(p(il));对于delta_X来说,价格变化为1/sqrt(P) - 1/sqrt(p(iu))。
- 当前价格低于流动性价格区间
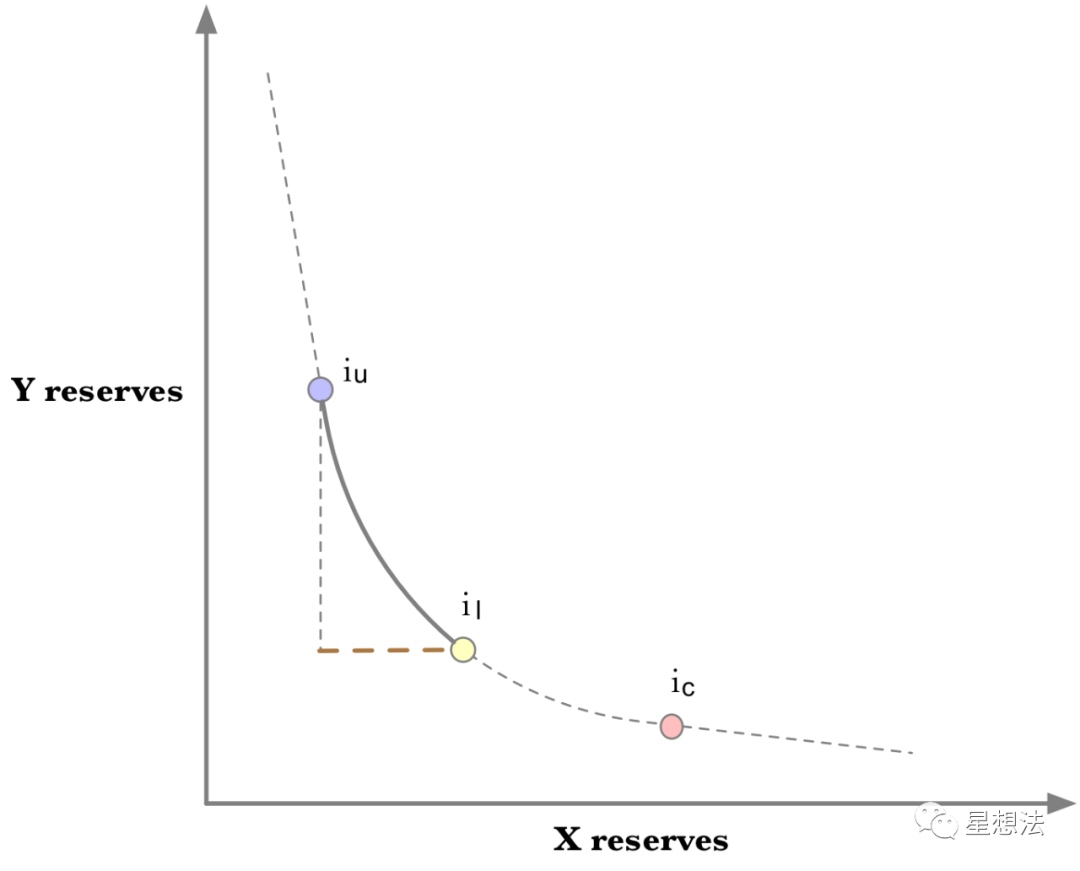
因为当前价格远低于il,即使从当前价格向iu滑动,也只需要x的资金,不需要y的资金。所以,在这种情况下,delta_Y = 0。因为从il滑向iu需要整个区间的x的资金,对于delta_X来说,价格变化为1/sqrt(il) - 1/sqrt(p(iu))。
- 当前价格高于流动性价格区间
和第一种情况类似,不重复分析了。
7 Swap交易费用
uniswap最复杂的逻辑是计算交易费用并分配。在添加和删除流动性之前需要将相应的交易费用提取。
-
Tick上的总流动性
在某个Tick上可以存在多个区间。在计算交易费用时,需要平摊这些费用给所有在这个Tick上多个区间的总的流动性。在每个区间的边界的Tick上记录下delta_L(所有以这个Tick为边界的区间的流动性总和)。
存在一个全局状态:liquidity,保存当前价格对应Tick的流动性总和。当价格波动,穿过某个Tick时,会进行流动性的增加或者减少(取决于价格波动方向)。举例来说,价格从左到右穿过区间,当穿过区间的第一个Tick时,流动性需要增加,穿出最后一个Tick时,流动性需要减少,中间的Tick都没有流动性的增加和减少(delta_L为0)。
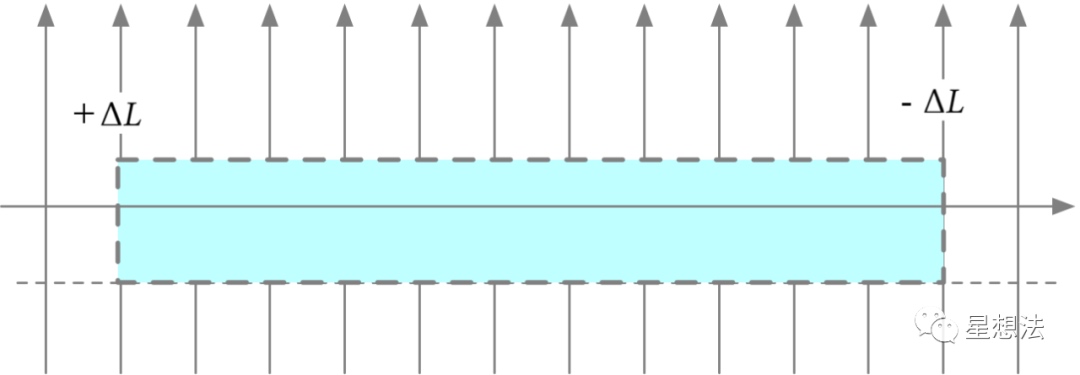
-
区间(Position)上的交易费用率
计算一个区间上的交易费用率,采用总的费用率减去区间外的费用率的方法。在一个区间的边界Tick上记录feeGrowthOutside。所谓的feeGrowthOutside,就是“另外”一个方向上总的费用率。另外的一个方向是相对穿过当前Tick的方向而言。当价格从左到右穿过一个Tick,feeGrowthOutside指的是Tick左边所有区间的费用率。简单的说,就是价格要去方向的相反方向所有区间的费用率。feeGrowthOutside用fo表示。因为fo是一个Tick的两个方向的总的费用率,两个方向的费用率的总和肯定是等于fg(全局的费用率)。所以当穿过一个Tick时,这个Tick上的fo要进行翻转:
$f_o(i)=f_g - f_o(i)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (6.20)$
当一个区间创建时,区间边界上Tick的fo需要初始化:
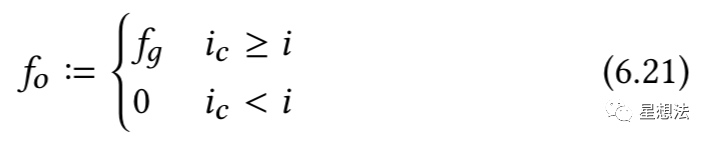
如果当前的价格大于Tick的价格时,因为即使当前价格在设置的区间内,但是之前费用也不会分到,所以,可以简单的假想为所有的费用发生在Tick价格之下,也就是fo=fg。如果Tick的价格大于当前价格,价格还没有穿过Tick,因为假设了之前所有发生的费用发生在Tick价格之下,Tick之上是没有费用的,所以fo=0。在理解了这些逻辑的基础上,在swap的过程中,随着价格的波动,一个区间上,超过最高Tick的费用率以及低于最低Tick的费用率可以用如下的方式计算:
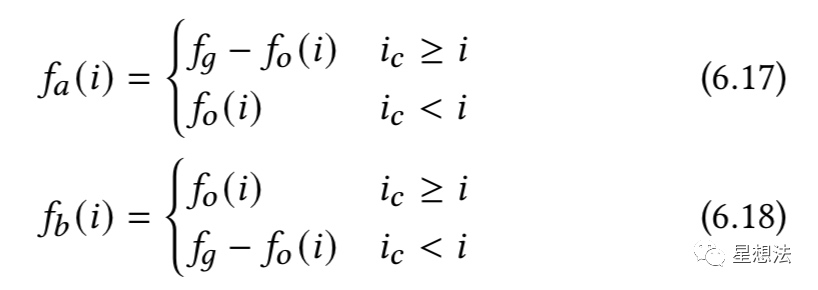
以低于最低Tick的费用率的计算为例,如果ic>=i (当前的价格是高于最低Tick的),低于Tick的所有的费用率就是fo(定义如此)。如果ic
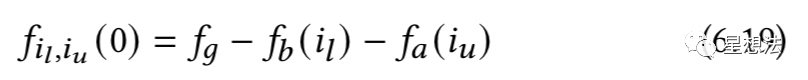
获取的费用率的基础上,用费用率乘以区间的流动性可以计算出该区间收取的费用。
总结:
uniswap V3版本核心思想是流动性集中。流动性提供者可以在某个区间提供流动性,提高资金使用率。在某个区间获取的交易费,由所有在该区间的流动性提供者均分。uniswap V3设计了区间粒度-Tick,并且推导了流动性添加/删除以及费用计算的过程。在之基础上,uniswap V3也更新了价格预言机的实现。

- sampleRate 81 浏览
- Leader的心跳信息 101 浏览
- cessssssssss 94 浏览
- 测试文章 141 浏览
- 智能合约开发语言 — Move 与 Rust 的对比 107 浏览
- 如何用 Solidity 创建一个“Hello World”智能合约 127 浏览
- Web3系列教程之进阶篇---8. IPFS实战 178 浏览
- C.R.E.A.M Hack with Yearn 102 浏览
- 零碎的Solidity小Tip 64 浏览
- 2372325 84 浏览
- 哈哈哈哈 59 浏览
- 测试文章 51 浏览
