彻底读懂零知识证明及其实现方法：解析zk-SNARK

我们已经越来越频繁地见到zk-SNARK，我们还会更多地遇到它。

大家都知道它是一种实现零知识证明的方法，也知道它是扩容和隐私方向的利器，但究竟什么是零知识证明，zk-SNARK 是如何实现零知识证明的？这便是本文试着去回答的问题。

阅读这篇文章需要保持较高的专注度，以及适当思考；但本文尽力做到没有含混和晦涩之处，所以如果你保持专注，看完就能理解零知识证明究竟是如何通过zk-SNARK 做到的，而不是停留在只知道概念的阶段。

那么现在，开始吧。

第一阶段： 为使用zk-SNARK 做准备工作

1. 把零知识证明的需求转换为数学运算电路

保险机构需要知道用户的一个体检数据是否达标，用户只想让保险机构知道数据是否达标，但不透露具体的数据给他们。怎么去做？

假设这个体检的隐私数据是x，x 的值在0\~7 之间（包含0和7）为达标，否则为不达标。那要做首先是把这个需求转换为一个可计算的问题，即有一个程序，其输入为x，当x 在0\~7 之间时，输出「真」，当x 不在该区间时，输出「假」。

该程序的计算过程可以被表达为如下一组方程的验证过程。当输入x 后，如果这4 个方程都能被满足，也就是方程左边的计算结果都为0，就能证明x 在0~7 之间，那么就输出「真」，否则输出「假」。这4 个方程为：

b0 * (b0-1)= 0 

b1 * (b1-1)= 0

b2 * (b2-1)= 0

2^0 * b0 + 2^1 * b1+2^2 * b2 – x = 0

注：b0、b1、b2的值由x确定，它们也是输入；前3 个方程约束b0、b1、b2的值为0或1；最后1个方程验证x的取值在0~7之间。

可以把这样的一组方程表达为一个数学运算电路。以b0 * (b0-1) 为例，它这一部分的电路如下图所示。

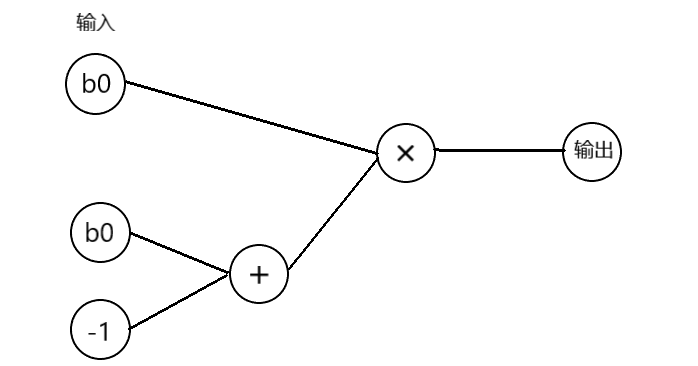
而整个程序的计算过程可以抽象表达为下图：

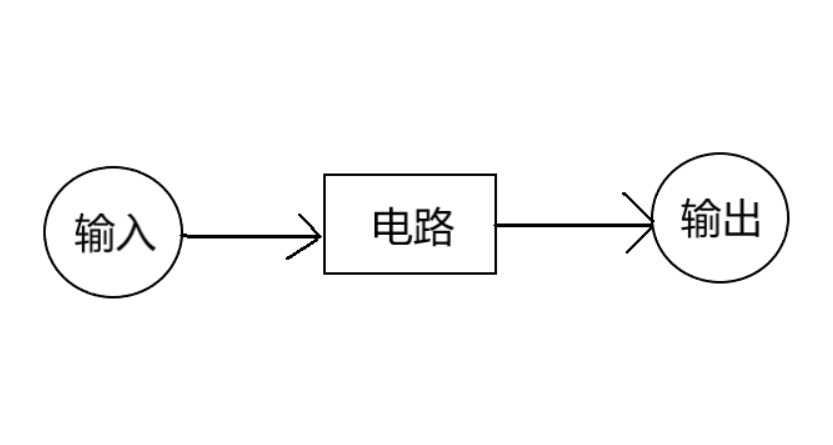
如此一来，零知识证明的问题就被转化为「输入+用作证明的数学运算电路+输出」；如果输出为真，就可以相信输入为真。在本文的例子中，如果输出为0，就可以相信用户的体检数据达标。

2. 把数学运算电路转换为多项式

在把零知识证明的需求转换为数学运算电路后，我们能够把验证者和证明者这两个角色分开。而当验证者不是证明者时，就创造了一个可以隐藏输入（原始数据）的机会。

随之而来问题只有一个：验证者凭什么相信这个「输出」是「输入」通过「用作证明的数学运算电路」计算出来的？最简单的办法就是验证者看着证明者输入和计算，但这样就无法隐藏输入了。

所以我们要在数学运算电路的基础上接着做转换，把输入、用作证明的数学运算电路、输出这三者绑定到一起，也就是说，能够通过某种方式验证「输出」是否为「输入」通过「用作证明的数学运算电路」计算出来的。

这样一来，在输出为真的前提下，只要该验证通过，证明者就可以相信输入为真。

为了完成这种绑定，需要把数学运算电路转换为多项式。

(以下为数学转换过程，若无兴趣可跳至下一张图片下方的段落)

首先要把数学运算电路转换为一阶约束系统（RICS）。

Vitalik 在《Quadratic Arithmetic Programs: from Zero to Hero》一文中详细介绍了这个转换过程，本文为省略细节描述，将直接引用Vitalik 使用的例子。

这是一个数学的过程，我们只需要知道这种转换是等价的即可，若希望知晓细节，可阅读Vitalik 的文章。

Vitalik的那组方程为：

x * x - sym_1 = 0
sym_1 * x – y = 0
(y + x) * 1 - sym_2 = 0
(sym_2 + 5) * 1 - ~out = 0

以其中的第一个方程x * x - sym_1 = 0 为例，它被转换为R1CS 后的形式如下所示：

a = [0, 1, 0, 0, 0, 0]
b = [0, 1, 0, 0, 0, 0]
c = [0, 0, 0, 1, 0, 0]
s = [~one,x,~out,sym_1,y,sym_2]

R1CS 是由上方3 个向量（a, b, c）组成的序列，解向量为s，且满足s. a s.b - s.c = 0，这也被称作一个约束。可以试着计算一下，你会发现s.a s.b - s.c = x * x - sym_1，它们是等价的。

Vitalik 的例子包含4 个拍平后的方程，每个方程对应一个RICS 约束，因此一共有4 个约束。

接下来是把R1CS 转换为多项式。依然不需要深入理解如何转换，只需要知道转换是等价的。转换过程如下：

一共有4 个RICS 约束，每个约束中都包含一个向量a，因此一共有4 个向量a，它们分别是：

a = [0, 1, 0, 0, 0, 0]
a = [0, 0, 0, 1, 0, 0]
a = [0, 1, 0, 0, 1, 0]
a = [5, 0, 0, 0, 0, 1]

通过拉格朗日插值法，可以把这4 个向量转换为6 个多项式（因为每个向量包含6个值），它们分别是：

–5+ 9.166* x- 5* x^2+0.833* x^3
8- 11.333 * x + 5 * x^2-0.666 * x^3
0 + 0 * x + 0 * x^2 + 0 * x^3
–6 + 9.5 * x - 4 * x^2 + 0.5 * x^3
4 - 7 * x + 3.5 * x^2 - 0.5 * x^3
–1+ 1.833 * x- 1 * x^2+ 0.166 * x^3

可以试着把x= 1代入这6 个多项式计算，将得到[0、1、0、0、0、0] 这6 个值，你会发现它们正是第一个约束下的向量a；把x 等于2、3、4分别带入这6 个多项式，将得到其他3 个约束下的向量a。

向量a 对应6 个多项式，向量b 和向量c 也是如此，因此一共会有18 个多项式。当x=1时，这18 个多项式的18 个解正是第一个约束；当x 等于2、3、4时，分别得到第2、3、4 个约束。多项式与RICS 是等价的。

到此就完成了从数学运算电路到多项式的转换：

• 通过RICS 转换，把证明多个原方程转换为证明多个s.a * s.b - s.c = 0 ；
• 通过多项式转换，把证明多个s.a s.b - s.c = 0 转换为证明在x=1、x=2、x=3、x=4 时，A(x) B(x) – C(x) = 0，其中A(x) = s.a，B(x) = s.b，C(x) = s.c。如下图所示。

图中最左边一行数字[1, 3, 35, 9, 27, 30] 为Vitalik 例子中的解向量s。A1(x)为a 的第1 个多项式在x 处的取值，比如A1(1)=0；A1(x)~A6(x) 构成第x 个约束的向量a，比如x=1时，a=[0、1、0、0、0、0]；其他同理。

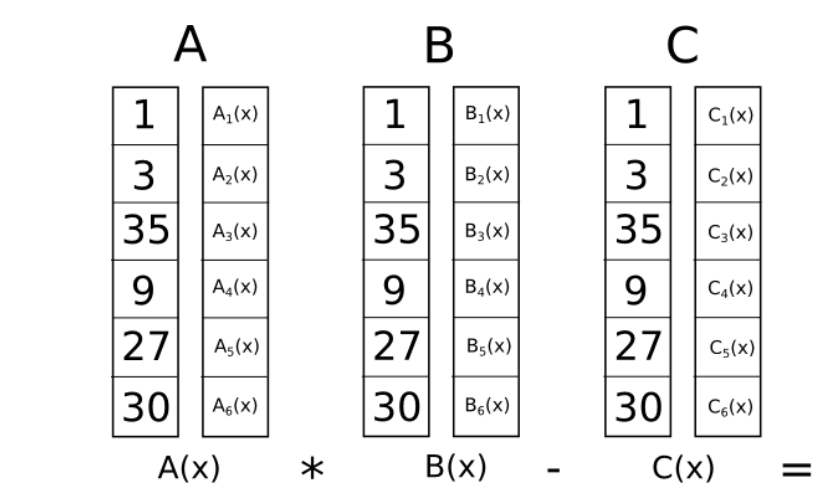
(若跳过转换，可从此处接着阅读)

我们似乎是在通过一个繁琐的步骤，把本来简单的证明变成了复杂的证明，为什么？如果你仔细观察，就会发现一件神奇的事情发生了：

本来验证者需要验证的是：输入通过用作证明的数学运算电路，输出为真；但现在验证者需要验证的是，当x=1、x=2、x=3、x=4时，A(x) * B(x)–C(x) = 0。

A(x) * B(x)–C(x) 中包含了解向量s，它是把输入、输出、电路绑定在一起的；验证A(x) * B(x)–C(x) = 0，就是在验证输入和输出是否满足用作证明的数学运算电路。

这便解决了本节开始时提出的问题：验证者凭什么相信「输出」是「输入」通过「用作证明的数学运算电路」计算出来的。

如此一来，验证者就不需要关注具体的输入和计算过程，只需要验证A(x) * B(x) – C(x) = 0本身是否成立。这让我们真正有了机会去隐藏输入。

到此处可以长舒一口气了，虽然还没开始进入zk-SNARK，但我们已经完成了最艰难的部分。如果转换部分没有理解清楚也没关系，你只需要知道：

通过zk-SNARK 实现零知识证明，实际上是要在zk-SNARK 的帮助下，验证当x= 1、2、3、……、n时，A(x) * B(x)–C(x) = 0，其中n 是RICS 约束的个数；而不同的零知识证明问题，区别只在于它们的A(x)、B(x)、C(x)不同。

3. 把多次验证转换为一次验证

对于包含n 个约束的零知识证明问题，需要进行n 次A(x) * B(x)–C(x)是否为零的验证。可不可以把n 次验证变为一次验证？可以。

• 定义t(x) = (x-1) (x-2) …… * ( x-n)，t(x)在x=1、x=2、…… 、x=n 处必然等于零；
• 那么如果有一个多项式h(x)，使得A(x) B(x)–C(x) = t(x) h(x)成立，便意味着A(x) * B(x)–C(x) 这个多项式可以被t(x)整除，那么这个多项式在x=1、x=2、…… 、x=n 处也必然等于零。

也就是说，验证A(x) * B(x)–C(x) = t(x) * h(x)，就能够一次完成全部RICS 约束的验证；而一旦这个验证通过，就可以相信输入为真。

现在终于可以把接力棒交给zk-SNARK 了，它要做的工作就是帮助验证 A(x) B(x)–C(x) = t(x) h(x)。

验证的过程是怎样的？很简单。verifier（验证者）选择一个随机数x 发起挑战，prover（证明者）证明在这个 x 处，A(x) * B(x)–C(x) = t(x) * h(x)。

在不知不觉中，一件关键又有趣的事情发生了：

证明者本来需要证明在x=1、x=2、…… 、x=n 时，A(x) * B(x)–C(x) = 0，这是一种推理式证明，就像我们解数学题，需要一步步地推导和计算，在这种证明过程中，要隐藏解题的知识是困难的。

但现在，推理式证明变成了交互式证明：verifier 在一个随机点上提出挑战，prover 给出这个点上的解响应挑战；prover 需要有「知识」才能计算出随机点上的解，但这个解本身不会泄露「知识」。

而这，就是零知识证明得以成立的前提，或者说，如果没有交互式证明这种证明方法，零知识证明这个领域便不会存在。

接下来只剩下一个问题：为什么能通过验证多项式上的一个点来确定两个多项式A(x) B(x)–C(x) 与t(x) h(x)是否相等？

这是由多项式的特性决定的，「一个多项式在任意点的计算结果都可以看做是其唯一身份的表示」。（引自Maksym）

用图形说明更为直观。下图是两个多项式，蓝色曲线是f(x) = x^3– 6 x^2+ 11 x– 6，绿色曲线是f(x) = x^3– 6 x^2+ 10 x– 5，不难发现，两个多项式只有微小的不同，但它们的曲线却是迥异的。

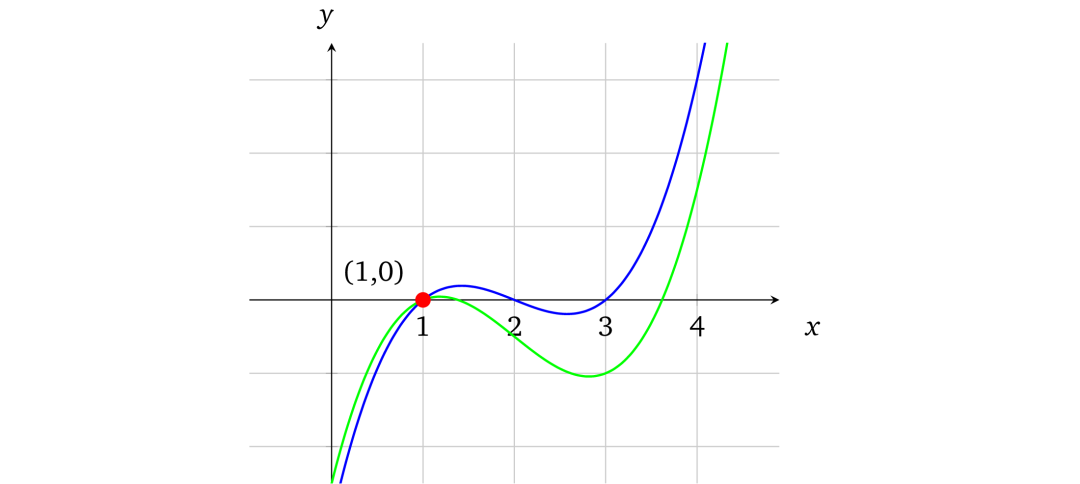
就像世界上没有两片相同的树叶，世界上也没有会在某个区域重合的两条不同曲线，它们只会在有限的点上相交。对于两个阶数为d（x的最大指数）的多项式，它们相交的点数不会超过d。

在本文的应用中，有一个多项式A(x) B(x)–C(x)，一个多项式t(x) h(x)，如果它们不相等，它们只会在最多d 个点上相交，也就是在d个点上的解相同。

这意味着只有当验证者选择的随机挑战点x 恰好是这d 个点中的一个时，才有可能发生误判，即在A(x) B(x)–C(x) 与 t(x) h(x)不相同的情况下误以为它们相同。

误判的概率存在，但我们不用为此担心，比较d 个点和x 的取值范围，这件事发生的概率极低；结合后续在zk-SNARK 协议中使用的密码学方法，这件事可以被认为几乎不可能发生。

那么现在，在全部的准备工作完成后，本文进入下一个阶段。对第一阶段的抽象总结就是：零知识证明的问题就是验证计算满足多个约束的问题，而多项式可以一个点验证多个约束。

第二阶段：使用zk-SNARK 完成零知识证明

得益于交互式证明和多项式的特性，我们可以通过验证挑战点x 上多项式A(x) B(x)–C(x)的解与t(x) h(x)的解是否相等来验证A(x) B(x)–C(x) = t(x) h(x)是否成立，这种方式是可以隐藏A(x) * B(x)–C(x)这个多项式的系数的。

多项式的系数就是零知识证明中的「知识」，最明显的，这个系数里是包含了想要隐藏的秘密输入（解向量s）的。

使用zk-SNARK 完成零知识证明，就是完成verifier 给出随机点进行挑战的工作和prover 给出随机点上的解完成证明的工作，这实际上是互不信任的verifier 和prover 之间的一场攻防战，他们使用的武器是密码学。

1. verifier 加密挑战点

分析需要被验证的A(x) B(x)–C(x) = t(x) h(x)：

• t(x)是verifier 和prover 双方都知道的一个多项式，t(x) = (x-1) (x-2) …… * ( x-n)；

• A(x) * B(x) – C(x)只有prover 知道，它的系数包含着知识；

• h(x)也只有prover 知道，是用A(x) B(x) – C(x)除以t(x)计算出来的，h(x)不能被verifier 知道，因为可以通过t(x)和h(x) 计算出A(x) B(x) – C(x)。

为了清晰起见，先把A(x) B(x)–C(x)写为p(x)，把要证明的问题简化为证明p(x) = t(x) h(x)。

其证明过程包含如下3 步：

• verifier 选择随机挑战点x，假设x= r；
• prover 收到r 后，计算p(r)和h(r)，并把这两个值给verifier；
• verifier 计算t(r)，然后计算t(r) h(r)，并判断t(r) h(r) = p(r)是否成立，若成立，则验证通过。

这实际上就是zk-SNARK 的基础工作流程，但直接这样做会有一个问题：

prover 是知道t(x)的，如果把r 给他，他就能够计算出t(r)，那么他完全可以构造出一对假的p(x) 和h(x)，使得p(r)= t(r) * h(r)，结果就是他虽然不知道真正的p(x)，却能骗过verifier。

解决这一问题的办法就是对r 加密，使得prover 可以计算某种形式下p(r)和h(r)，但却不能通过该形式下的t(r)构造假的满足验证要求的p(x) 和h(x)。

观察prover 的证明过程，他需要计算p(x) 和h(x)这两个多项式，但不管哪一个，其形式均为：c0+ c1x^1+ ……+ cnx^n；prover 本身知道c0、c1等等全部系数。

如果verifier 把x 给prover，假设x= s，prover 就能完成全部计算；但如果verifier 把加密后的s 给prover，prover 是不能完成计算的，因为他无法用加密后的s 计算出s^2、……、s^n。

所以当verifier 确定随机点s 后，需要把加密后的s、s^2、……、s^n 全部给prover，这样prover 才能完成计算。

在实际应用中，verifier 是把E(s)、E(s^2)、……、E(s^n)给到prover，其中E(s)是s 的加密值，E(s) = g^s (mod n)，这是一种同态加密方法。

同态加密有一个性质，就是先加密后计算的解与先计算后加密的解与是相同的。也就是说：

• c0+ c1E(s)+ ……+ cnE(s^n) = g^(c0+ c1s^1+ ……+ cns^n）；
• 即，p(E(s)) = E(p(s)) = g^p(s)，h(E(s)) = E(h(s)) =g^h(s)；
• 那么，prover 就能通过计算p(E(s)) 和h(E(s))，得到g^p(s) 和g^h(s)。

此处只需要知道这种计算确实可行即可，如果想了解密码学部分的工作原理，可看我之前的一篇文章，《一文读懂零知识证明背后的简单逻辑》。

所以现在，证明过程变成了如下3 步：

• verifier 选择随机挑战点x，假设x= s，然后把一整套s 的加密值给prover；

• prover 收到后，计算g^p(s) 和g^h(s)，并把这两个值给verifier；

• verifier 计算t(s)，然后计算(g^h(s))^ t(s)，并判断(g^h(s))^t(s) = g^p(s)是否成立，若成立，则验证通过，因为这意味着h(s) * t(s) = p(s)。

通过对随机点s 加密，可以避免prover 作弊，但prover 还有一个漏洞可钻，即他不使用verifier 给出的挑战点s 计算h(s) 和t(s)，而是用其他值计算并欺骗verifier。

所以verifier 还需要一个方法，该方法能够证明prover 给出的值确实是用s 计算出来的。

本文将不具体展开这一部分，简单而言就是verifier 除了选择随机数s 外，还要选择一个随机数α，prover 给出的解需要维持s 和α 之间的关系，如果这个关系被破坏了，则证明他没有用s 在计算。

该方法被称作指数知识假设，若想了解具体内容，可阅读Maksym 的文章。

在verifier 完成了他的防守战后，轮到prover 了。

2. prover 加密计算结果

虽然prover 只把多项式在挑战点x 上的解给了verifier，但如果多项式系数的取值范围较小，verifier 是有可能通过暴力破解从解计算出多项式系数，即知识的。因此，prover 需要对解加密。

证明过程变成如下3 步：

• verifier 选择随机挑战点x，假设x= s，以及随机数α，然后把一整套s 的加密值、以及一整套α * s 的加密值给prover；
• prover 收到后，计算g^p(s)、g^h(s)、g^(αp(s))；选择随机数δ 对解加密，变为(g^p(s))^δ、(g^h(s))^δ、(g^(αp(s)))^δ；然后把这3 个加密值给verifier；
• verifier 计算t(s)，然后计算((g^h(s))^δ)^t(s)，并判断((g^h(s))^δ)^t(s) = (g^p(s))^δ是否成立，若成立，则意味着h(s) * t(s) = p(s)；
• 与此同时，verifier 还需要验证((g^p(s))^δ)^α = (g^(α*p(s)))^δ是否成立，若成立，则证明prover 给出的解是用s 计算出来的。

如此一来，prover也就完成了自己的攻防战。

3. 从交互变为非交互

zk-SNARK 的N 是指Non-Interactive，即非交互，但不难发现在上述的证明过程中，是需要verifier 和prover 交互的，而且我们都知道，交互式证明本身是零知识证明得以成立的前提。那非交互是指什么？

很简单，所谓的非交互只不过是把verifier 选择随机数的工作交给了「可信设置」来完成，也就是由一个可信任的第三方在证明开始前选择随机挑战点x。

这种改变对prover 没什么影响，因为他需要的始终是一组与x 相关的加密值，而不用管这些加密值来自verifier，还是来自可信第三方。但这种改变对verifier 有影响，因为他本来知道x，可以用x 计算t(x)，但现在他不知道了。

所以从交互到非交互，最主要的改变就是要在可信设置中把t(x)给到verifier，以便他能完成验证工作。

t(x)需要被加密，因为prover 可以利用t(x)的值做弊；但加密后的t(x)又要能被用于计算，因为verifier 需要计算h(x) * t(x)。这便是这一部分的难点所在：h(x) 和t(x)都是加密值，但之前使用的同态加密方法不支持两个加密值的乘法。

zk-SNARK 使用配对操作解决这一问题，用公式表达就是e(g^a, g^b)= a^g b^g=（a b）^g，其中g^a 和g^b 是加密值。配对操作可以把两个加密值映射为它们的乘积。

可信设置通过该方法把t(x)给到verifier。于是，证明过程变为如下3 步：

• 可信设置：可信第三方选择随机挑战点x，假设x= s，以及随机数α，然后把一整套s 的加密值、以及一整套α * s的加密值给prover；再把t(s) 的加密值g^t(s)和α 的加密值g^α给verifier；
• prover 收到后，计算g^p(s)、g^h(s)、g^(αp(s))；选择随机数δ 对解加密，变为(g^p(s))^δ、(g^h(s))^δ、(g^(αp(s)))^δ；然后把这3 个加密值给verifier；
• verifier 计算并判断e(g^p, g) = e(g^t(s), g^h)是否成立，若成立，则意味着h(s) * t(s) = p(s)；g^p、g^h、g^p′ 为prover 提供的3 个加密值的简写。
• 与此同时，verifier 还需要验证e(g^p′ , g) = e(g^p, g^α)是否成立，若成立，则证明prover给出的解是用s计算出来的。

到这一步，我们就基本完成了zk-SNARK 协议的构造工作，它可以在不泄露多项式系数的情况下证明多项式，即实现零知识证明。

额外一提，在可信设置阶段为prover 和verifier 准备的加密值被称作CRS （common reference string），用以生成CRS 的随机数是要被销毁的，它们可用于作弊；可信设置需要可信第三方，通过什么机制选择可信第三方是一个议题。

可信设置影响zk-SNARK 的通用性，因此也发展出了不需要可信设置的zk-SNARK，其意义重大但理解起来并不难：只不过是换了一种方式提供随机挑战点x。

不管有多少种zk-SNARK，我们需要知道的是：零知识证明是一种交互式的证明系统，对它而言重要的、也是与安全和资源相关的一个工作就是，以什么样的方式提供随机挑战点。

4. 把p(x)还原为A(x) * B(x)–C(x)

zk-SNARK 协议需要证明的多项式是A(x) B(x)–C(x)，如果把p(x)还原为A(x) B(x)–C(x)，相较于p(x)时的协议，主要区别在于：

• prover 需要分别提供A(s)、B(s)、C(s)的加密值；
• verifier 需要验证A(s) B(s) = h(s) t(s)+ C(s)；
• 在对prover 的计算进行约束时（比如必须用s 计算），需要有3 个不同的α 分别对应于A(s)、B(s)、C(s)；当prover 对计算结果加密时，需要有3 个不同的δ分别加密A(s)、B(s)、C(s)。

在具体的zk-SNARK 协议中，还会通过一些设计来改进协议，本文不再一一论述，zk-SNARK 的探秘之旅到这里就全部结束啦。

在旅程结束之际，有几点说明：

1. zk-SNARK 有不同的组合实现方法，本文主要是以 Pinocchio 协议为线索；密码学所涉甚广，文章难免会有疏漏和理解不当之处，请不要尽信，深入研究需以论文为参考。

2. 本文在构建zk-SNARK 协议部分（第二部分）采用了Maksym 文章的框架；Maksym 的文章极有条理地介绍了zk-SNARK，但可能对于不太具备相关背景知识的读者来说仍有一定的理解难度，这也是我写这篇文章的原因所在。

那么，如果你读到了这里，谢谢你；如果你在知晓零知识证明的整个实现过程后，被其中的数学之美打动，那我太开心了。

参考

1. 东泽；浅谈零知识证明：背景与起源

2. Vitalik Buterin；《Quadratic Arithmetic Programs: from Zero to Hero》，

https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649

3. Maksym Petkus；《Why and How zk-SNARK Works: Definitive Explanation》，https://arxiv.org/pdf/1906.07221.pdf；

中文版本：从零开始学习 zk-SNARK（一）——多项式的性质与证明，翻译：even@安比实验室，校对：valuka@安比实验室

4. 李画；一文读懂零知识证明背后的简单逻辑

撰文：李画

致谢：东泽、even

*参考：Maksym Petkus，*Why and How zk-SNARK Works: Definitive Explanation

原文：https://mp.weixin.qq.com/s/riDH6UBr1sJxnk-V48KAhQ