区块链中的数学 - RSA运算中的快速幂模运算
- blocksight
- 发布于 2020-07-12 18:36
- 阅读 894
本节主要介绍了RSA运算中的快速幂模运算,是RSA算法的核心。
写在前面
上一节介绍了RSA的共模攻击和低指数攻击,这一节我们继续说RSA的计算方面的注意的问题。 由于RSA主要计算过程是幂运算和模运算,但是RSA参数选取都是很大的整数, 没有概念的可以看看上一篇中的代码例子,e,n是一长串的大整数,直接进行指数运算再取模是不可行的。实际实现中用到的是快速幂模运算。快速幂运算是快速幂模运算的基础,所以现先讲下快速幂运算。
快速幂运算
一般计算 循环累乘的算法时间复杂度是O(n)级别,而快速幂能做到O(logn)。 快速幂利用到了指数的二进制分解的规律。下面来看看代码实现(Java)
int Pow(int a, int b)
{
int ans = 1;
while (b)
{
if (b & 1)
ans *= a ;
a *= a;
b >>= 1;
}
return ans;
}比较简洁。通过分析一个实例来理解思路。 假设b = 7 = 0111(二进制) , 求$ a^7=a^{1+2+4} a^{2^0+2^1+2^2} a^{2^0} a^{2^1} a^{2^2}$ 将b变成2的指数形式的和, 任何整数都可以用二进制表示,所以是通用的表示法。
代码中a *= a; 得到 $a^{2^2},a^{2^4} ...$
代码中b >>= 1; 是每次向左移二进制位,然后判断末尾是奇数时候,a乘以前位的结果,即代码中的ans.
这就是if语句的处理过程。
总体上并不难以理解,快速幂算法能够帮助我们算出指数非常大的幂,传统的求幂算法之所以时间复杂度非常高,是因为当指数n非常大的时候,需要执行的循环操作次数也非常大。
所以快速幂算法的核心思想就是每一步都把指数缩小一半( b >>= 1 等价于b/2),而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小,所需要执行的循环次数也变小。
快速幂模运算
快速幂模运算是指求$a^b$ mod n的一类运算。 如果理解了快速幂运算,快速幂模运算就很好懂了,快速幂模运算 = 快速幂 + 模运算。 快速幂模运算又称蒙哥马利算法(Montgomery modular multiplication) 下面看下代码:
int PowMod(int a, int b, int c)
{
int ans = 1;
a %= c;
while (b)
{
if (b & 1)
ans = (ans * a) % c;
a = (a * a) % c;
b >>= 1;
}
return ans;
}这里用到了模运算性质: ab mod c = (a mod c)(b mod c) mod c 注:关于模运算其他更多性质参照历史文章在运算过程中取模,减少了数据的规模。有了这些基础,我们再回过头来看e的选择。
e参数选择
在RSA原理一节中,我们说e的值通常取 65537 = $2^{16}$+ 1
不信的话可以自己检查一下电脑里的cert证书,下图是一个例子。
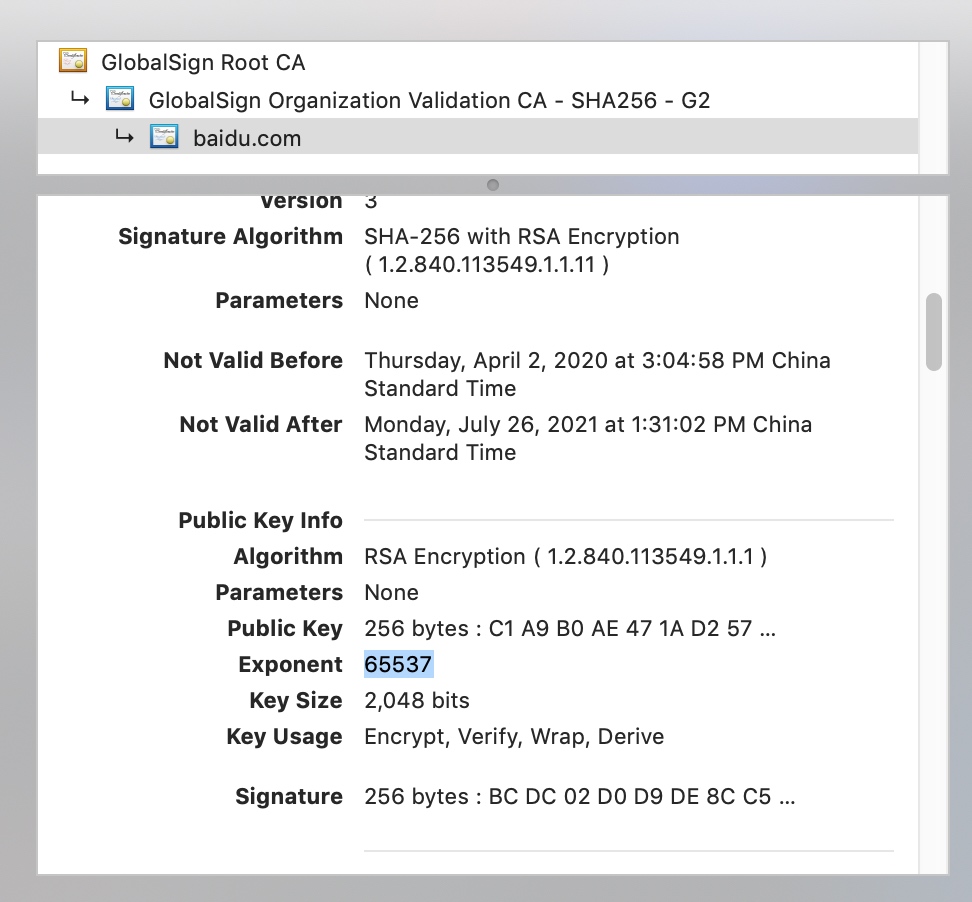
为什么选择这个特定的数呢? 首先是个素数, 其次二进制表示10000000000000001 只有两个1,代码只有两次需要执行if语句的乘法,很大限度地提高了运算使用公钥的运算速度。 可见实际应用实现中参数的选择需要仔细斟酌,幸运的是现在成熟的库已经有了很成熟的实现,大家只要用好就可以。
小结
本节主要介绍了RSA运算中的快速幂模运算,是RSA算法的核心。RSA计算方面的优化还有其他一些细节,这里不做探讨了,感兴趣的可以自己探索。 通过这几篇的介绍,我们可以知道,实现RSA算法不是简单按照原理就可以了,从理论到实用工程化,考虑的因素很多,成熟的实现库如OpenSSL,Java的bouncycastle等都是增加了前面说的随机填充等内容来达到实用安全的目的。
到此我们讲了两种应用最广的公钥密钥体制:椭圆曲线密码体制和RSA。 之前一文章也提到了公钥加密标准PKCS,有必要说一下这个规范。
好了,下一篇继续说公钥加密标准PKCS。
欢迎关注公众号:blocksight
- 区块链中的数学--PLookup 553 浏览
- 区块链中的数学 -- MultiSet check& Schwartz–Zippel lemma 493 浏览
- 区块链中的数学 - 环签名(ring signature) 834 浏览
- 区块链中的数学 -盲签名(Blind Signature) 1057 浏览
- 区块链中的数学 - sigma协议OR Proof&签名 632 浏览
- 区块链中的数学 - sigma协议与Fiat-Shamir变换 820 浏览
- 区块链中的数学 - 何谓零知识证明? 683 浏览
- 区块链中的数学 - RSA累加器的非成员证明 650 浏览
- 区块链中的数学 -- Accumulator(累加器) 1100 浏览
- 区块链中的数学--Merkle树承诺 926 浏览
- 区块链中的数学 - Kate承诺batch opening 738 浏览
- 区块链中的数学 - Kate承诺 971 浏览
