区块链中的数学-Uniwap自动化做市商核心算法解析

写在前面

上一节说了secp256k1签名可锻性以及解决方案， 熟悉椭圆曲线原理的话，应该会有较好理解。

题外话：
最近又有一些朋友赞赏了文章，非常感谢，后续有可能会推出一些权益类的活动【或产品】，这些支持者将会优先【或者免费或者优惠】获取，计划将赞赏者信息放到GitHub上来统一展示，像其他的开源项目一样，以示感谢。

好了，回到正题，本节我们看一下unsiwap的自动化做市商算法，这里我们不打算介绍uniswap的一般性概念以及如何操作等【互联网上很容易找到】，重点关注核心算法。

常量乘积做市商模型

Uniswap协议采用的是常量乘积做市商模型，又称为“恒定乘积做市商模型“。数学公式表示为 x * y = k, 通过确定某一时刻x,y的兑换比例，来实现x和y之间的自动交易。所有规则定义在合约中，由区块链系统（如以太坊）自动执行，省去第三方做市商参与， 有时也称为：x-y-k自动做市商模型。

x-y-k模型

x-y-k模型中，x, y分别一个交易对（Pair/Pool）中某一时间两种代币的余额，x,y 对应值两种不同的代币，在目前uniswap版本中，目前只支持ERC20代币。

在x和y做代币交换时，如果没有交易费用，x * y 恒定等于k，是不变的。

即代币交换价格由x与y的比值决定，从而保证了xy乘积不变。也就是说，当你出售 ∆x代币时，你将得到∆y代币，这样 x * y =（x + ∆x） (y − ∆y）。
因此，价格（∆x / ∆y）是 x / y的函数。具体而言，当你将∆x与∆y交易时，兑换代币余量更新如下：

$x' = x + ∆x = (1 + \alpha ) * x$
$y' = y - ∆y = (1 - \beta) * y$

上式中，添加∆x换取∆y

$\alpha= ∆x / x \ ,\ \beta = ∆y / y$

要使得交换后乘积不变，即x' * y' = x * y ,那么：

$1+\alpha=\frac{1}{1-\beta }$

由此可推出下式：

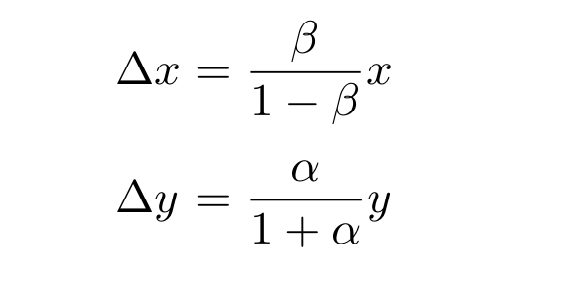
最终在没有手续费的情况下两种代币余量：

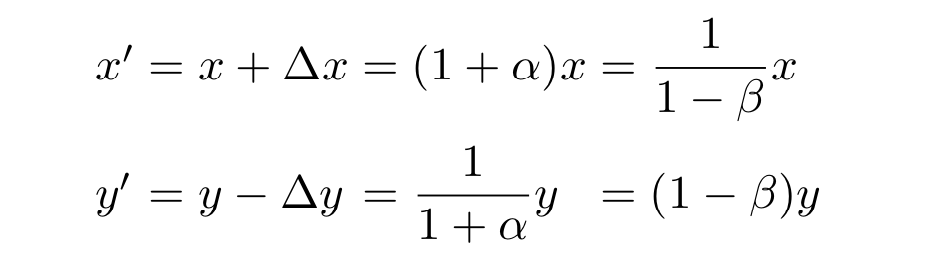
从上面的公式可以看出，变化前（xy）和变化后（x' y'）是相等的。

添加费用机制的x-y-k模型

现在考虑每一笔代币交易要收取一定的费用。设0 ≤ ρ < 1为费用，例如，对于0.3%的费用表，ρ = 0.003。
新的模型计算公式变化为：

$x' = x + ∆x = (1 + \alpha （1 - ρ ）) * x$

$y' = y - ∆y = (1 -\beta ) * y$

其中依然$\alpha = ∆x / x, \beta= ∆y / y$, 同样，要使得交换后乘积不变，即x' * y' = x * y ,那么：
$1 + \alpha （1 - ρ ）=\frac{1}{1-\beta }$

可得出：

$\Delta x =\frac{\beta }{1-\beta } *\frac{1}{1-\rho } * x$

$\Delta y=\frac{\alpha (1-\rho)}{1+\alpha(1-\rho )} * y$

简化公式，令 $\gamma = 1 - \rho$ ,可得：

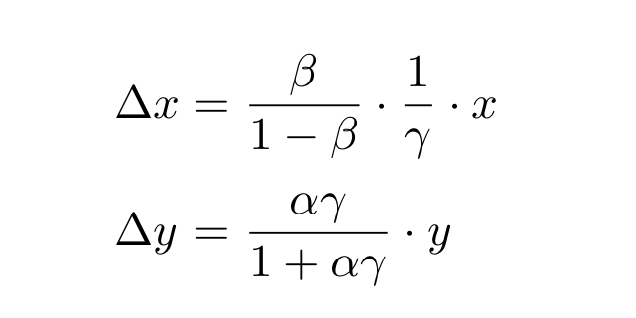
可以看到当$\gamma = 1$时，上式退化成没有费用的情况。 引入$\gamma$后，$x'_p , y'_p$表示交易池中最终的储量变化如下：

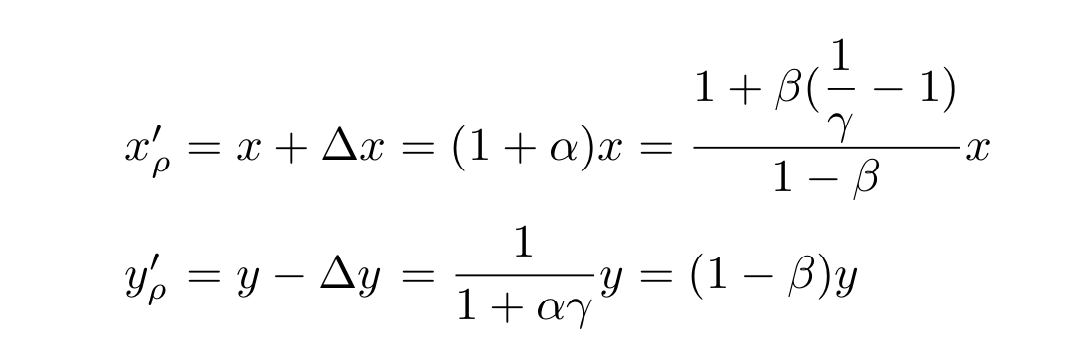
可以看到，有了交易费用，$x'_p * y'_p$略微增大，这是因为一部分x作为费用，没有参与恒定乘积计算，而放到了储备池中。
具体增加多少呢？定量为：

$1+\beta(\frac{1}{\gamma }-1)$

倍与xy。 同样 $\gamma = 1$ 简化为无费用模式。

uniswap的流动性生成体现出乘积k的作用， 使用$\sqrt{k}$ 作为流动性增长的依据，下一篇会详细说明。

小结

本文内容主要参考：
https://github.com/runtimeverification/verified-smart-contracts/blob/uniswap/uniswap/x-y-k.pdf
https://uniswap.org/whitepaper.pdf

uniswap 做市商模型简单而优雅，运行近两年没有出现大的安全问题。从本节的分析中可以看到，并无高等数学积分，离散，分布等内容，高中数学水平就能理解，这也印证了简洁的力量。

回首这些年区块链历史，很多复杂模式(算法)的Defi(区块链)项目消逝在区块链（defi）的社会大实验中，包括很多被认为得高价值项目（明星项目），不得不让人深思：

是不是越是平实的技术越容易落地与发展？

这让我想到了著名华人物理学家张首晟的名言：
”the final truth must be simple, beautiful and universal“

后面的分析文章中，我们依然能够感受到这种简洁的魅力。

下一节继续分析uniswap中交易以及添加移除流动性对价格产生的影响。

欢迎关注公众号：blocksight